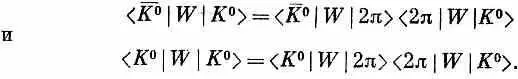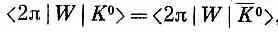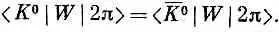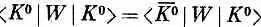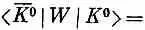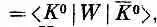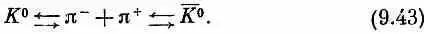
Из существования таких реакций следует, что есть амплитуда, которую мы обозначим через 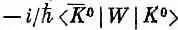 , превращения К 0 в
, превращения К 0 в 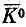 , обусловленная тем самым слабым взаимодействием, с которым связан распад на два p-мезона. Ясно, что есть и амплитуда обратного процесса
, обусловленная тем самым слабым взаимодействием, с которым связан распад на два p-мезона. Ясно, что есть и амплитуда обратного процесса 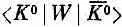 . Так как материя и антиматерия ведут себя одинаково, то эти две амплитуды численно равны между собой; мы обозначим их через А:
. Так как материя и антиматерия ведут себя одинаково, то эти две амплитуды численно равны между собой; мы обозначим их через А:
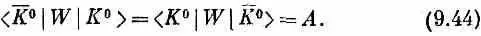
И вот, сказали Гелл-Манн и Пайс, здесь возникает интересная ситуация. То, что люди назвали двумя разными состояниями мира (К 0 и 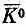 ), на самом деле следует рассматривать как одну систему с двумя состояниями, потому что имеется амплитуда перехода из одного состояния в другое. Для полноты рассуждений следовало бы, конечно, рассмотреть не два состояния, а больше, потому что существуют еще состояния 2л и т. д.; но поскольку наши физики интересовались главным образом связью К 0 с
), на самом деле следует рассматривать как одну систему с двумя состояниями, потому что имеется амплитуда перехода из одного состояния в другое. Для полноты рассуждений следовало бы, конечно, рассмотреть не два состояния, а больше, потому что существуют еще состояния 2л и т. д.; но поскольку наши физики интересовались главным образом связью К 0 с 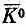 , то они не захотели усложнять положения и представили его приближенно в виде системы с двумя состояниями. Другие состояния были учтены в той мере, в какой их влияние неявно скажется на амплитудах (9.44).
, то они не захотели усложнять положения и представили его приближенно в виде системы с двумя состояниями. Другие состояния были учтены в той мере, в какой их влияние неявно скажется на амплитудах (9.44).
В соответствии с этим Гелл-Манн и Пайс анализировали нейтральную частицу как систему с двумя состояниями. Начали они с того, что выбрали состояния | К 0 > и | 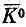 > за базисные состояния. (С этого места весь рассказ становится очень похожим на то, что было для молекулы аммиака.) Всякое состояние |y> нейтрального K -мезона можно тогда описать, задав амплитуды того, что оно окажется в одном из базисных состояний. Обозначим эти амплитуды
> за базисные состояния. (С этого места весь рассказ становится очень похожим на то, что было для молекулы аммиака.) Всякое состояние |y> нейтрального K -мезона можно тогда описать, задав амплитуды того, что оно окажется в одном из базисных состояний. Обозначим эти амплитуды
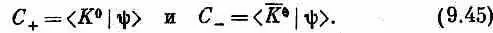
Следующим шагом мы должны написать уравнение Гамильтона для такой системы с двумя состояниями. Если бы К 0 и 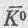 не были бы связаны между собой, то уравнения выглядели бы просто
не были бы связаны между собой, то уравнения выглядели бы просто
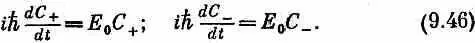
Однако есть еще амплитуда 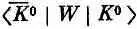
перехода К 0 в 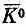 ; поэтому в правую часть первого уравнения надо еще добавить слагаемое
; поэтому в правую часть первого уравнения надо еще добавить слагаемое
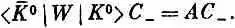
Аналогичное слагаемое АС +надо добавить и в уравнение, определяющее скорость изменения С _. Но это еще не все! Если уж мы учитываем двухпионный эффект, то надо учесть и то, что существует еще дополнительная амплитуда превращения К 0в самого себя по цепочке
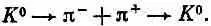
Эта дополнительная амплитуда (обозначим ее 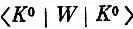 ) в точности равна амплитуде
) в точности равна амплитуде 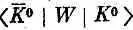
, так как амплитуды перехода в пару p-мезонов или от пары p-мезонов в К 0 или 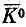 одни и те же.
одни и те же.
Если угодно, можно показать это и подробнее. Прежде всего напишем
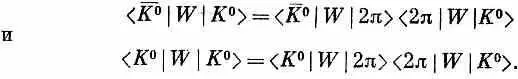
Симметрия между материей и антиматерией требует, чтобы
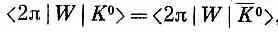
а также
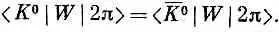
Отсюда
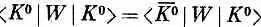
а также
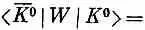
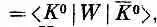
Читать дальше

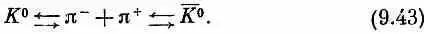
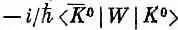 , превращения К 0 в
, превращения К 0 в 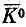 , обусловленная тем самым слабым взаимодействием, с которым связан распад на два p-мезона. Ясно, что есть и амплитуда обратного процесса
, обусловленная тем самым слабым взаимодействием, с которым связан распад на два p-мезона. Ясно, что есть и амплитуда обратного процесса 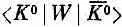 . Так как материя и антиматерия ведут себя одинаково, то эти две амплитуды численно равны между собой; мы обозначим их через А:
. Так как материя и антиматерия ведут себя одинаково, то эти две амплитуды численно равны между собой; мы обозначим их через А: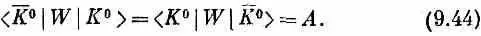
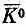 ), на самом деле следует рассматривать как одну систему с двумя состояниями, потому что имеется амплитуда перехода из одного состояния в другое. Для полноты рассуждений следовало бы, конечно, рассмотреть не два состояния, а больше, потому что существуют еще состояния 2л и т. д.; но поскольку наши физики интересовались главным образом связью К 0 с
), на самом деле следует рассматривать как одну систему с двумя состояниями, потому что имеется амплитуда перехода из одного состояния в другое. Для полноты рассуждений следовало бы, конечно, рассмотреть не два состояния, а больше, потому что существуют еще состояния 2л и т. д.; но поскольку наши физики интересовались главным образом связью К 0 с 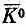 , то они не захотели усложнять положения и представили его приближенно в виде системы с двумя состояниями. Другие состояния были учтены в той мере, в какой их влияние неявно скажется на амплитудах (9.44).
, то они не захотели усложнять положения и представили его приближенно в виде системы с двумя состояниями. Другие состояния были учтены в той мере, в какой их влияние неявно скажется на амплитудах (9.44).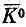 > за базисные состояния. (С этого места весь рассказ становится очень похожим на то, что было для молекулы аммиака.) Всякое состояние |y> нейтрального K -мезона можно тогда описать, задав амплитуды того, что оно окажется в одном из базисных состояний. Обозначим эти амплитуды
> за базисные состояния. (С этого места весь рассказ становится очень похожим на то, что было для молекулы аммиака.) Всякое состояние |y> нейтрального K -мезона можно тогда описать, задав амплитуды того, что оно окажется в одном из базисных состояний. Обозначим эти амплитуды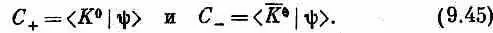
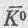 не были бы связаны между собой, то уравнения выглядели бы просто
не были бы связаны между собой, то уравнения выглядели бы просто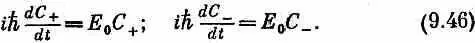
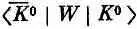
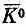 ; поэтому в правую часть первого уравнения надо еще добавить слагаемое
; поэтому в правую часть первого уравнения надо еще добавить слагаемое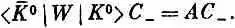
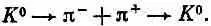
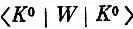 ) в точности равна амплитуде
) в точности равна амплитуде 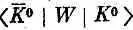
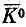 одни и те же.
одни и те же.