Feynmann - Feynmann 8

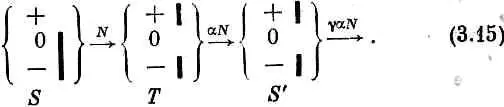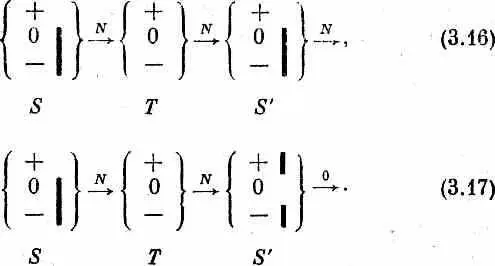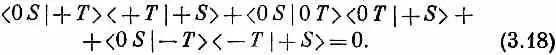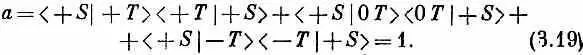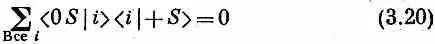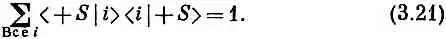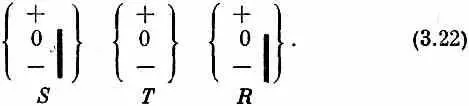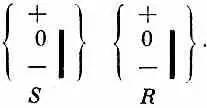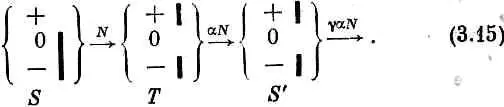
Теперь предположим, что мы повторили оба эти опыта, убрав из Т все перегородки. Тогда мы получим следующий замечательный результат:

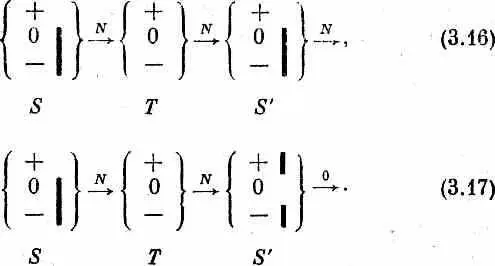
В первом случае через S ' прошли все атомы, во втором — ни одного! Это один из самых великих законов квантовой механики. То, что природа действует таким образом, вовсе не самоочевид­но; результаты, которые мы привели, отвечают в нашем идеа­лизированном случае квантовомеханическому поведению, на­блюдавшемуся в бесчисленных экспериментах.

§ 5 . Ннтерферирующив амплитуды

Как же это может быть, что, когда переходят от (3.15) к (3.17), т. е. когда открывается больше каналов, через фильтры начинает проходить меньше атомов? Это и есть старый, глубо­кий секрет квантовой механики — интерференция амплитуд. С такого рода парадоксом мы впервые встретились в интерферен­ционном опыте, когда электроны проходили через две щели. Помните, мы тогда увидели, что временами кое-где получается меньше электронов, когда обе щели открыты, чем когда открыта одна. Численно это получается вот как. Можно написать ам­плитуду того, что атом пройдет в приборе (3.17) через Т и S ' в виде суммы трех амплитуд — по одной для каждого из трех пучков в Т; эта сумма равна нулю:

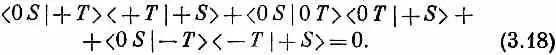
Ни одна из трех отдельных амплитуд не равна нулю: например, квадрат модуля второй амплитуды есть ga [см. (3.15)], но их сумма есть нуль. Тот же ответ получился бы, если бы мы настро­или S ’ на то, чтобы отбирать состояние (- S ). Однако при рас­положении (3.16) ответ уже другой. Если обозначить амплитуду прохождения через Т и S ' буквой а, то в этом случае мы будем иметь

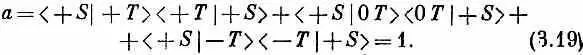
В опыте (3.16) пучок сперва расщеплялся, а потом восста­навливался. Как мы видим, Шалтая-Болтая удалось собрать обратно. Информация о первоначальном состоянии (+ S ) со­хранилась — все выглядит так, как если бы прибора Т вовсе не было. И это будет верно, что бы ни поставили за «до отказа раскрытым» прибором Т. Можно поставить за ним фильтр R — под каким-нибудь необычным углом — или что-угодно. Ответ будет всегда одинаков, как будто атомы шли в S ' прямо из пер­вого фильтра S .

Итак, мы пришли к важному принципу: фильтр Т или любой другой с открытыми до отказа заслонками не приводит ни к каким изменениям. Надо только упомянуть одно добавочное условие. Открытый фильтр должен не только пропускать все три пучка, но и не вызывать в них неодинаковых возмущений. Например, в нем не должно быть сильного электрического поля близ одного из пучков, которого не было бы возле других. Причина заключается вот в чем: хотя это добавочное возмуще­ние может и не помешать всем атомам пройти сквозь фильтр, оно может привести к изменению фаз некоторых амплитуд. Тогда интерференция стала бы не такой, как была, и амплитуды (3.18) и (3.19) стали бы другими. Мы всегда будем предполагать, что таких добавочных возмущений нет.

Перепишем (3.18) и (3.19) в улучшенных обозначениях. Пусть i обозначает любое из трех состояний (+ Т), (0 Т ) и (- Т ); тогда уравнения можно написать так:

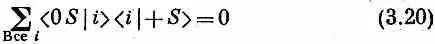
и

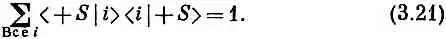
Точно так же в опыте, в котором S ' заменяется совершенно произвольным фильтром R , мы имеем

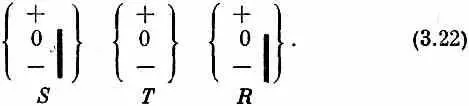
S Т R Результаты будут всегда такими же, как если бы прибор Т убрали и осталось бы только

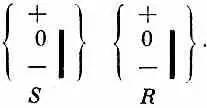
Или на математическом языке