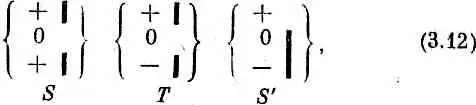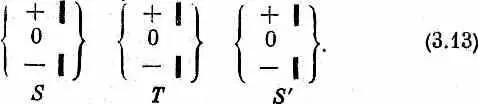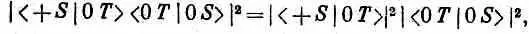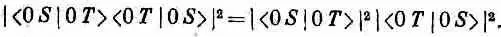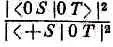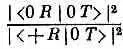Feynmann - Feynmann 8

§ 3. Последовательно соединенные фильтры Штерна — Герлаха

Пусть у нас есть атомы, отфильтрованные в состояние (+ S ), которые мы затем пропустили через второй фильтр, переведя, скажем, в состояние (О Т), а затем — через другой фильтр (+ S ). (Обозначим его S ', чтобы не путать с первым фильтром S .) Вспомнят ли атомы, что они уже раз были в со­стоянии (+ S )? Иначе говоря, мы ставим такой опыт:

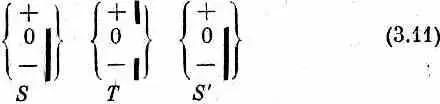
и хотим знать, все ли атомы, прошедшие сквозь Т, пройдут и сквозь S ' . Нет. Как только они пройдут фильтр Т, они сразу же позабудут о том, что, входя в Т, они были в состоянии (+ S ). Заметьте, что второй прибор S в (3.11) ориентирован в точности так же, как первый, так что это по-прежнему фильтр типа S . Состояния, выделяемые фильтром S ', — это, конечно, все те же (+ S ), (0 S ) и (- S ).

Здесь существенно вот что: если фильтр Т пропускает толь­ко один пучок, то та доля, пучка, которая проходит через второй фильтр S , зависит только от расположения фильтра Т и совер­шенно не зависит от того, что было перед ним. Тот факт, что те же самые атомы однажды уже были отсортированы фильтром S , никак и ни в чем не влияет на то, что они будут делать после того, как прибор Т снова отсортирует их в чистый пучок. От­сюда следует, что вероятность перейти в те или иные состояния для них одна и та же безотносительно к тому, что с ними слу­чалось до того, как они угодили в прибор Т, Для примера сравним опыт (3.11) с опытом

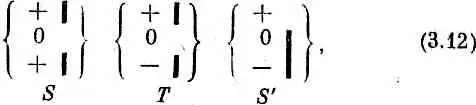
в котором изменилось только первое S . Пусть, скажем, угол a (между S и Т) таков, что в опыте (3.11) треть атомов, прошед­ших сквозь Т, прошла также и через S '. В опыте (3.12), хоть в нем, вообще говоря, через Т пройдет другое число атомов, но через S ' пройдет та же самая, часть их — одна треть.

Мы можем на самом деле показать, опираясь на то, чему мы научились раньше, что доля атомов, которые выходят из Т и проходят через произвольный определенный фильтр S ', зависит лишь от Т и S ' , а не от чего бы то ни было происходившего ра­нее. Сравним опыт (3.12) с

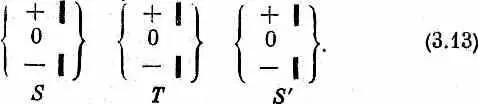
Амплитуда того, что атом, выходящий из S , пройдет и сквозь Т, и сквозь 6", в опыте (3.12) равна

< + S |0 T >< 0 T |0 S >.

Соответствующая вероятность такова:

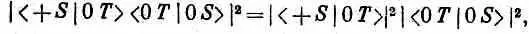
а вероятность в опыте (3.13)

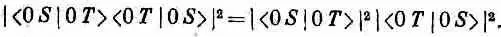
Их отношение

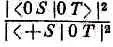
зависит только от Т и S ' и совсем не зависит от того, какой пу­чок (+ S ), ( 0 S ) или (- S ) был отобран в S . (Абсолютные же количества могут быть большими или меньшими, смотря по тому, сколько прошло через Т.) Мы бы получили, конечно, аналогичный результат, если бы сравнили вероятности того, что атомы перейдут в плюс- или минус-состояние (по отноше­нию к S '), или отношения вероятностей перейти в нуль- или минус-состояние.

Но раз эти отношения зависят только от того, какой пучок может пройти сквозь Т, а не от отбора, выполненного первым фильтром S , то становится ясно, что тот же результат получил­ся бы, если бы последний прибор даже не был фильтром S . Если в качестве третьего прибора (назовем его R ) мы используем прибор, повернутый относительно Т на некоторый произволь­ный угол, то все равно увидим, что отношения типа

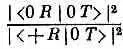
не зависят от того, какой пучок проник через первый фильтр S .

§ 4. Базисные состояния

Эти результаты иллюстрируют один из основных принципов квантовой механики: любая атомная система может быть раз­делена процессом фильтрования на определенную совокуп­ность того, что мы назовем базисными состояниями, и будущее поведение атомов в любом данном отдельном базисном состоя­нии зависит только от природы базисного состояния — оно не зависит от предыдущей истории. Базисные состояния за­висят, конечно, от примененного фильтра; например, три со­стояния (+ Т ), (0 Т) и (- Т)— это одна совокупность базисных состояний, а три состояния (+ S ), (0 S ) и (- S ) — другая. Возможностей сколько угодно, и ни одна не хуже другой.