Feynmann - Feynmann 7

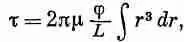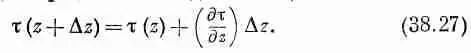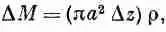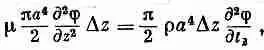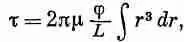
где интеграл берется от 0 до а — радиуса стержня. После ин­тегрирования получаем

Если закручивать стержень, то его момент оказывается про­порциональным углу и четвертой степени диаметра: стержень вдвое большего радиуса в шестнадцать раз жестче относительно кручения.

Прежде чем расстаться с кручением, рассмотрим применение теории к одной интересной задаче — волнам кручения. Возьмем длинный стержень и неожиданно закрутим один его конец; вдоль стержня, как показано на фиг. 38.10, а, пойдет волна кручения.

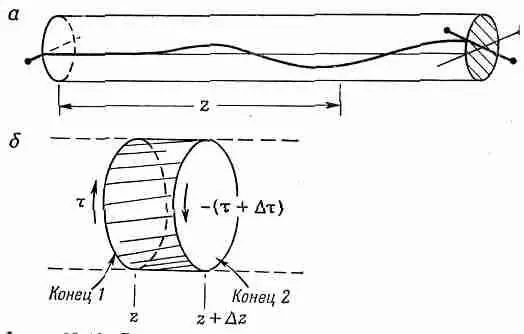
Фиг. 38.10. Волна кручения в стержне (а) и элемент объема стержня (б).

Это явление более интересно, нежели простое стати­ческое скручивание. Посмотрим, можем ли мы понять, как это происходит.

Пусть z — расстояние от некоторой точки до основания стержня. Для статического закручивания момент сил на всем протяжении стержня один и тот же и пропорционален j / L — полному углу вращения на полную длину. Но в нашей задаче важна местная деформация кручения, которая, как вы сразу поймете, равна д j / д z . Если кручение вдоль стержня неравно­мерное, то уравнение (38.25) следует заменить таким:

Посмотрим теперь, что же происходит с элементом длины Dz, который показан в увеличенном масштабе на фиг. 38.10, б. На конце 1 маленького отрезка стержня действует момент t(z), а на конце 2— другой момент сил t(z+Dz). Если величина Dz достаточно мала, то можно воспользоваться разложением в ряд Тэйлора и, сохранив только два члена, написать

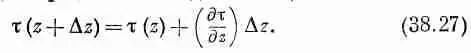
Полный момент сил Dt, действующий на маленький от­резок стержня между z и Dz, равен разности t(z) и

t(z+Dz),

или

Dt=( д t / д z)Dz.

Дифференцируя уравнение (38.26), получаем

Действие этого полного момента должно вызвать угловое ускорение отрезка стержня. Масса его равна

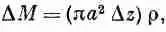
где r — плотность материала. В гл. 19 (вып. 2) мы нашли, что момент инерции кругового цилиндра равен mr 2/2; обо­значая момент инерции нашего отрезка через Dl, получаем

Закон Ньютона говорит нам, что момент силы равен произ­ведению момента инерции на угловое ускорение, или

Собирая теперь все воедино, находим

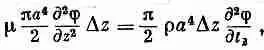
или

Вы, должно быть, уже узнали, что это такое: это одномерное волновое уравнение. Мы получили, что волны кручения распространяются по стержню со скоростью

Чем плотнее стержень при одной и той же жесткости, тем мед­леннее движется волна, а чем он жестче, тем волна бежит бы­стрее. Скорость ее не зависит от диаметра стержня.

Волны кручения представляют частный случай волн сдвига. Волны сдвига в общем случае — это такие волны, при которых деформация не изменяет объема любой части материала. В вол­нах кручения мы сталкиваемся с особым распределением нап­ряжений сдвига — они распределены по кругу. Но волны при любом распределении напряжений сдвига будут распростра­няться с одной и той же скоростью, которая определяется фор­мулой (38.32). Сейсмологи, например, обнаружили, что такие волны сдвига распространяются и внутри Земли.