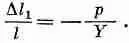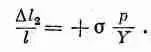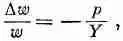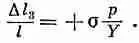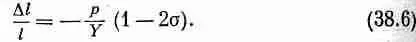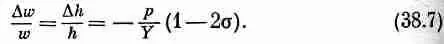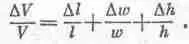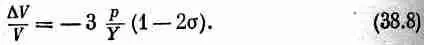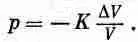Feynmann - Feynmann 7

§ 2. Однородная деформация

В качестве первого примера посмотрим, что происходит с пря­моугольным бруском при однородном гидростатическом сжатии. Давайте поместим брусок в резервуар с водой. При этом воз­никнет сила, действующая на каждую грань бруска и пропор­циональная его площади (фиг. 38.2).

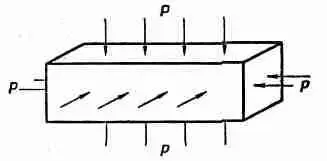
Фиг. 38.2. Брусок под действием равномерного гидростатического давления.

Поскольку гидростатиче­ское давление однородно, то напряжение (сила на единичную площадь) на каждой грани бруска будет одним и тем же. Прежде всего найдем изменение длины бруска. Его можно рассматри­вать как сумму изменений длин, которые происходили бы в трех независимых задачах, изображенных на фиг. 38.3.

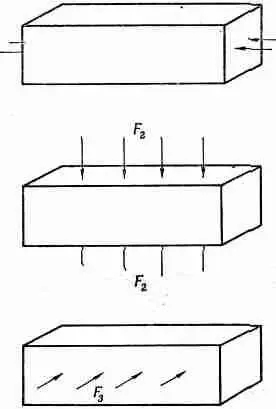
Фиг. 38.3. Гидростатическое давление равно суперпозиции трех сжатий.

Задача 1 . Если мы приложим к концам бруска давление р, то деформация сжатия будет отрицательна и равна p / Y :

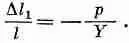
Задача 2 . Если мы надавим на горизонтальные грани бруска, то деформация по высоте будет равна - p / Y , а соответствующая деформация в бо­ковом направлении будет +s p / Y . Мы получаем

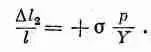
Задача 3 . Если мы прило­жим к сторонам бруска дав­ление р, то деформация дав­ления снова будет равна p / Y , но теперь нам нужно определить деформацию длины. Для этого боковую деформа­цию нужно умножить на -s. Боковая деформация равна

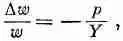
так что

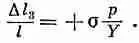
Комбинируя результаты этих трех задач, т. е. записывая Dl как dl 1+Dl 2+Dl 3, получаем

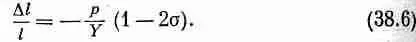
Задача, разумеется, симметрична во всех трех направлениях, поэтому

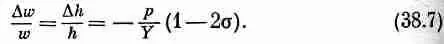
Интересно также найти изменение объема при гидроста­тическом давлении. Поскольку V=lwh, то для малых пере­мещений можно записать

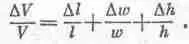
Воспользовавшись (38.6) и (38.7), мы имеем

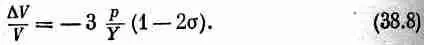
Имеются любители назы­вать DV/V объемной де­формацией и писать

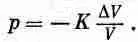
Объемное напряжение р (гидростатическое давление) пропор­ционально вызванной им объемной деформации — снова закон Гука. Коэффициент К называется объемным модулем и связан с другими постоянными выражением

Поскольку коэффициент К представляет некоторый практиче­ский интерес, то во многих справочниках вместо Y и s приво­дятся У и К. Но если вам нужно знать а, то вы всегда можете получить это значение из формулы (38.9). Из этой формулы видно также, что коэффициент Пуассона s должен быть меньше 1/ 2. Если бы это было не так, то объемный модуль К был бы от­рицательным и материал при увеличении давления расширялся бы. Это позволило бы добывать механическую энергию из лю­бого кубика, т. е. это означало бы, что кубик находится в неу­стойчивом равновесии. Если бы он начал расширяться, то рас­ширение продолжалось бы само по себе с высвобождением энергии.

Посмотрим, что получится, если мы приложим к чему-то «косое» напряжение. Под косым, или скалывающим, напряже­нием мы подразумеваем такое воздействие, как показано на фиг. 38.4.