Feynmann - Feynmann 7

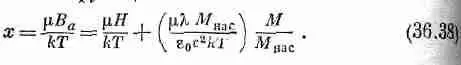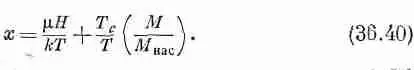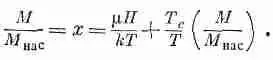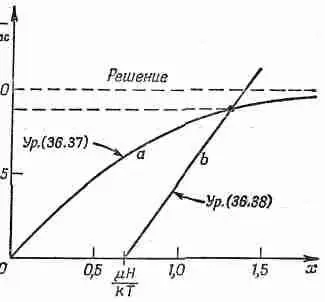
Фиг. 36.13. Графическое реше­ние уравнений (36.37) и (36.38),

Воспользовавшись еще уравнением (36.36) для В а , можно записать х как функцию от М:

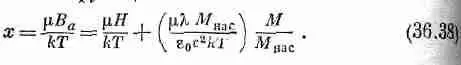
Эта формула определяет линейную зависимость между М/М нас и х при любой величине Н. Прямая пересекается с осью х в точке x = m H / kT , и наклон ее равен e 0 с 2 kT / m l КМ нас . Для любого частного зна­чения Н это будет пря­мая, подобная прямой b на фиг. 36.13. Пересечение кривых а и о дает нам решение для М/М нас. Итак, задача решена.

Посмотрим теперь, годны ли эти решения при различных обстоятельствах. Начнем с H =0. Здесь представляются две возможности, показанные кривыми b 1 и b 2 на фиг. 36.14.

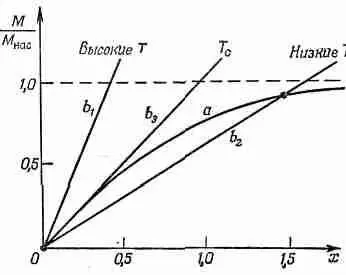
Фиг . 36.14. Определение намагниченности при Н=0.

Обра­тите внимание, что наклон прямой (36.38) пропорционален аб­солютной температуре Т. Таким образом, при высоких темпера­турах получится прямая, подобная b 1 Решением будет только М/М нас=0. Иначе говоря, когда намагничивающее поле Я равно нулю, намагниченность тоже равна нулю. При низких температурах мы получили бы линию типа b 2и стали возможны два решения для М/М нас: одно М/М нас=0, а другое М/М наспорядка единицы. Оказывается, что только второе решение устойчиво, в чем можно убедиться, рассматривая малые вариа­ции в окрестности указанных решений.

В соответствии с этим при достаточно низких температурах магнитные материалы должны намагничиваться спонтанно. Короче говоря, когда тепловое движение достаточно мало, то взаимодействие между атомными магнитиками заставляет их выстраиваться параллельно друг другу, получается постоянно намагниченный материал, аналогичный пос­тоянно поляризованным сегнетоэлектрикам, о которых мы говорили в гл. 11 (вып. 5).

Если мы отправимся от высоких температур и начнем дви­гаться вниз, то при некой критической температуре, называемой температурой Кюри Т c , неожиданно проявляется ферромагнит­ное поведение. Эта температура соответствует на фиг. 36.14 линии b 3 , касательной к кривой а, наклон которой равен еди­нице. Так что температура Кюри определяется из равенства

При желании уравнение (36.38) можно записать в более прос­том виде через Т c :

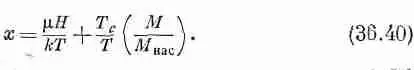
Что же получается для малых намагничивающих полей Н? Из фиг. 36.14 нетрудно понять, что получится, если нашу пря­мую линию сдвинуть немного направо. В случае низкой темпе­ратуры точка пересечения немного сдвинется направо по слабо наклоненной части кривой а и изменения М будут сравнительно невелики. Однако в случае высокой температуры точка пересе­чения побежит по крутой части кривой а и изменения М станут относительно быстрыми. Эту часть кривой мы фактически мо­жем приближенно заменить прямой линией а с единичным наклоном и написать

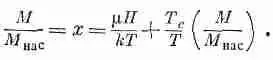
Теперь можно разрешить уравнение относительно М/М нас :

Мы получаем закон, несколько напоминающий закон для па­рамагнетизма:

Отличие состоит, в частности, в том, что мы получили намагни­ченность как функцию Н, с учетом взаимодействия атомных магнитиков, однако главное то, что намагниченность обратно пропорциональна разности температур Т и Т с , а не просто абсолютной температуре Т. Пренебрежение взаимодействием между соседними атомами соответствует l=0, что, согласно уравнению (36.39), означает Т с = 0. Результат при этом полу­чится в точности таким же, как и в гл. 35.