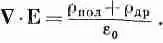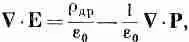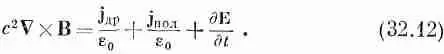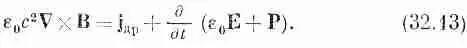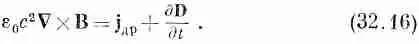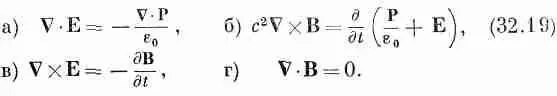Feynmann - Feynmann 7

Сегодня же мы предпочитаем обозначать через r полную плотность зарядов, включая в нее и заряды, связанные с инди­видуальными атомами. Если назвать эту часть зарядов r пол, то можно написать

r=r пол+r др,

где r др— плотность зарядов, учтенная Максвеллом и относя­щаяся к другим зарядам, не связанным с определенными атомами. При этом мы бы написали

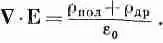
После подстановки r полиз (32.9) получаем

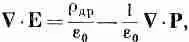
или

В плотность тока, фигурирующую в уравнениях Макс­велла для СX B, вообще говоря, тоже вносится вклад от связанных атомных электронных токов. Поэтому мы можем написать

j= j пол+ j др,

причем уравнение Максвелла приобретает вид

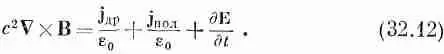
Используя уравнение (32.10), получаем

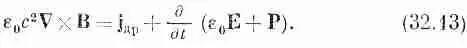
Теперь вы видите, что если бы мы определили новый вектор D

D=e 0 E+ P, (32.14)

то два уравнения поля приняли бы вид

С· D=r др(32.15)

и

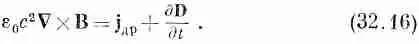
Это и есть та форма уравнений, которую использовал Мак­свелл для диэлектриков. А вот и остальные два уравнения:

СX Е=- д B/ д t

и

С· B=0,

которые в точности совпадают с нашими.

Перед Максвеллом и другими учеными того времени вставала проблема магнетиков (за них мы вскоре примемся). Они ничего не знали о циркулирующих токах, ответственных за атомный магнетизм и поэтому, в плотности тока утеряли еще одну часть. Вместо уравнения (32.16) они на самом деле писали

где Нотличается от e 0с 2 В, так как последнее учитывает эффекты атомных токов. (При этом j 'представляет то, что осталось от то­ков.) Таким образом, у Максвелла было четыре полевых век­тора: Е, D , Ви Н, причем в Dи Нскрывалось то, на что он не обратил внимания,— процессы, происходящие внутри вещест­ва. Уравнения, написанные в таком виде, вы встретите во мно­гих местах.

Чтобы решить их, необходимо как-то связать Dи Нс дру­гими полями, поэтому зачастую писали

D = e E

и

В= m H .(32.18)

Однако эти связи верны лишь приближенно для некоторых ве­ществ, и то лишь когда поля не изменяются слишком быстро со временем. (Для синусоидально изменяющихся полей зачастую можно писать уравнения таким способом, считая при этом e и m комплексными функциями частоты, но для произволь­ных изменений поля со временем это неверно.) На какие только ухищрения не пускаются ученые, чтобы решить уравнения! А мне кажется, что правильнее всего оставить уравнения запи­санными через фундаментальные величины, как мы понимаем их теперь, т. е. как раз то, что мы и проделали.

§ 3. Волны в диэлектрике

Теперь нам предстоит выяснить, какого сорта электро­магнитные волны могут существовать в диэлектрическом ве­ществе, где других зарядов, кроме тех, что связаны в атомах,

нет. Таким образом, мы возьмем r=-С· Р и j= д P/ д t . При этом уравнения Максвелла примут такой вид:

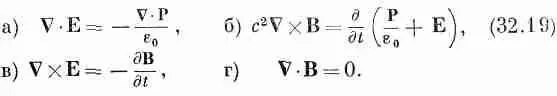
Мы можем решить эти уравнения, как делали это прежде. Начнем с применения к уравнению (32.19в) операции ротора:

СX(СX E)=-( д / д t)СX B.

Используя затем векторное тождество

СX(СX E) = С(С· E)-С 2 E и подставляя выражение для СX Bиз (32.19б), получаем