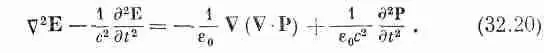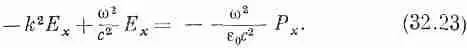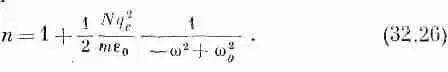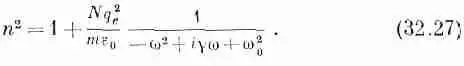Feynmann - Feynmann 7

Используя уравнение (32.19а) для С· Е, находим

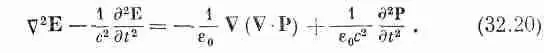
Таким образом, вместо волнового уравнения мы теперь полу­чили, что даламбертиан Еравен двум членам, содержащим по­ляризацию Р.

Однако Рзависит от Е, поэтому уравнение (32.20) все еще допускает волновые решения. Сейчас мы будем ограничиваться изотропными диэлектриками, т. е. Рвсегда будет иметь то же направление, что и Е. Попробуем найти решение для волны, движущейся в направлении оси z. Электрическое поле при этом будет изменяться как е i( w t - kz ). Предположим также, что волна поляризована в направлении оси х, т. е. что электрическое поле имеет только x-компоненту. Все это записывается следую­щим образом:

E x=E 0e i ( w t - kz ). (32.21)

Вы знаете, что любая функция от (z- vt ) представляет вол­ну, бегущую со скоростью v . Показатель экспоненты в выраже­нии (32.21) можно переписать в виде

-ik[z-(w/k)t],

так что выражение (32.21) представляет волну, фазовая ско­рость которой равна

v фаз=w/k.

В гл. 31 (вып. 3) показатель преломления n определялся нами из формулы

v фаз=c/n.

С учетом этой формулы (32.21) приобретает вид

Ex = E 0 e i w ( t - nz / c ) .

Таким образом, показатель n можно определить, если мы най­дем ту величину k, которая необходима, чтобы выражение (32.21) удовлетворяло соответствующим уравнениям поля, и затем воспользуемся соотношением

n = kc / w . (32.22)

В изотропном материале поляризация будет иметь только x-компоненту; кроме того, Рне изменяется с изменением коор­динаты х, поэтому С· P=0 и мы сразу же избавляемся от пер­вого члена в правой стороне уравнения (32.20). Вдобавок мы считаем наш диэлектрик «линейным», поэтому Р х будет изме­няться как е i w t и d 2 P x / dt 2 = - w 2P x. Лапласиан же в уравне­нии (32.20) превращается просто в д 2 E x / dz 2 =- k 2 Е x , так что в результате получаем

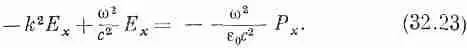
Теперь на минуту предположим, что раз Еизменяется си­нусоидально, то Рможно считать пропорциональной Е, как в уравнении (32.5). (Позднее мы вернемся к этому предположе­нию и обсудим его.) Таким образом, пишем

P x = e 0 N a E x .

При этом Е х выпадает из уравнения (32.23), и мы находим

k 2 = w 2 / c 2 (1+ N a ). (32.24)

Мы получили, что волна вида (32.21) с волновым числом k , задаваемым уравнением (32.24), будет удовлетворять уравне­ниям поля. Использование же выражения (32.22) для показате­ля n дает

n 2= l+Na. (32.25)

Сравним эту формулу с тем, что получилось у нас для пока­зателя преломления газа (гл. 31, вып. 3). Там мы нашли урав­нение (31.19), которое тогда имело вид

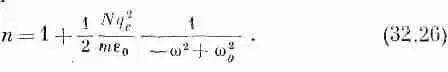
Формула (32.25) после подстановки w из (32.6) дает

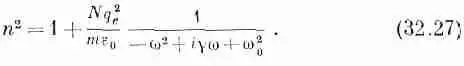
Что здесь нового? Во-первых, появился новый член igw, возникший в результате учета поглощения энергии в осцилля­торах. Во-вторых, слева вместо n теперь стоит n 2 и, кроме того, отсутствует дополнительный множитель 1 / 2 . Но заметьте, что если значение N достаточно мало, так что n близок к единице (как это имеет место в газе), то выражение (32.27) говорит, что n 2 равен единице плюс некое малое число, т. е. n 2=1+e. При этом условии мы можем написать, что n=Ц(1+e)»l+e/2, и оба выра­жения оказываются эквивалентными. Таким образом, наш но­вый метод дает для газа тот же самый, найденный нами ранее результат.

Теперь можно надеяться, что выражение (32.27) должно давать показатель преломления и для плотных материалов. Но по некоторым причинам оно нуждается в модификации. Во-первых, при выводе этого уравнения предполагалось, что поля­ризованное поле, действующее на каждый из атомов,— это поле Е х . Однако такое предположение неверно, поскольку в плотном материале существуют и другие поля, создаваемые соседними атомами, которые могут быть сравнимы с Е х . Анало­гичную задачу мы уже рассматривали при изучении статических полей в диэлектрике (см. гл. 11, вып. 5). Вы, вероятно, помните, что мы нашли поле, действующее на отдельный атом, представив его сидящим в сферической полости в окружающем диэлектрике. Поле в такой полости (мы назвали его локальным) увеличивается по сравнению со средним полем Ена величину Р/3e 0. (Не за­будьте, однако, что этот результат, строго говоря, справедлив только для изотропного материала, а также в случае куби­ческого кристалла.)