Feynmann - Feynmann 7

В качестве примера рассмотрим этот тензор не в веществе, а в пустом пространстве с электромагнитным полем. Вы знаете, что поток энергии электромагнитного поля описывается век­тором Пойнтинга S=e 0c 2 EX В. Так что х-, у- и z-компоненты вектора Sс релятивистской точки зрения являются компонентами: S ix , S t н и S tz нашего тензора энергии-импульса. Симметрия тензора S ij переносится и на временные компоненты, так что четы­рехмерный тензор S m vтоже симметричен:

S m v = S v m . . (31.29)

Другими словами, компоненты S xt , S yt , S zt , которые представ­ляют плотности х-, у- и z-компонент импульса, равны также х-, у- и z-компонентам вектора Пойнтинга S, или, как мы ви­дели раньше из других соображений, вектора потока энергии.

Оставшиеся компоненты тензора электромагнитного напря­жения S m v тоже можно выразить через электрическое и магнит­ное поля Еи В. Иначе говоря, для электромагнитного поля в пустом пространстве мы должны допустить существование тензора напряжений, или, выражаясь менее таинственно, по­тока импульса электромагнитного поля. Мы уже обсуждали это в гл. 27 (вып. 6) в связи с уравнением (27.21), но тогда мы не входили в детали.

Тем из вас, кто хочет испытать свою удаль на четырехмер­ных тензорах, может понравиться выражение для тензора S m v через поля:

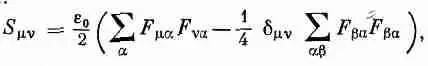
где суммирование по a и b проводится по всем их значениям (т. е. t , x , у и z ), но, как обычно в теории относительности, для суммы S и символа d принимается специальное соглашение. В суммах слагаемые со значками х, у, z должны вычитаться, а d tt=+1, тогда как d xx.=d уу= d zz=-1 и d m v=0 для всех m№ v (с=1). Сможете ли вы доказать, что эта формула приводит к плотности энергии S tt =( e 0 /2)( E 2 + B 2 ) и вектору Пойнтинга e 0 ЕX В? Можете ли вы показать, что в электростатическом поле, когда В=0, главная ось напряжения направлена по электриче­скому полю и вдоль направления поля возникает натяжение ( e 0 /2) E 2 и равное ему давление в направлении, перпендикуляр­ном направлению поля?

* Если не полагать с=1, как это делается здесь, то плотность энергии в принятых в книге единицах будет равна ( e 0 /2)( E 2 + с 2 B 2 ) или в единицах СИ 1 / 2 [ e 0 E 2 +( l / m 0 ) B 2 ]. — Прим. ред.

* Эту работу, затраченную на создание поляризации электрическим полем, не нужно путать с потенциальной энергией — p 0 * Е постоянного дипольного момента p 0 в поле Е.

* Обычно для коэффициентов пропорциональности между Р и Е пользуются термином тензор восприимчивости, оставляя термин поля­ризуемость для величин, относящихся к одной частице. Прим. ред.

* В гл. 10, следуя общепринятому соглашению, мы писали Р= e 0 c Е и величину c (хи) называли «восприимчивостью». Здесь же нам удобнее пользоваться одной буквой, так что вместо e 0 c мы будем писать a . Для изо­тропного диэлектрика a =( c -1 ) e 0 , где c — диэлектрическая проницаемость (см. гл. 10 §4 вып.5)

Глав a 32

ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА

§ 1. Поляризация вещества

§ 2. Уравнения Максвелла в диэлектрике

§ 3. Волны в диэлектрике