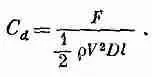t=t'D/V. (41.20)
В наших новых переменных производные в уравнении (41.18) тоже изменятся: так, д/дх перейдет в ( 1 / D )(д/дх') и т. д., так что уравнение (41.18) превратится в
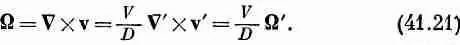
А наше основное уравнение (41.17) перейдет в
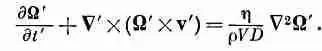
Все постоянные при этом собираются в один множитель, который мы, следуя традиции, обозначим через 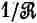 :
:

Если теперь мы просто запомним, что все наши уравнения должны выписываться для величин, измеряемых в новых единицах, то все штрихи можно опустить. Тогда уравнения для потока примут вид
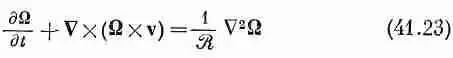
и
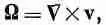
с условиями ,
v=0 , для
х 2 +у 2 = 1 / 4 (41.24)
и
v x=1, v y=v z=0
для
x 2+y 2+z 2>>1.
Что все это значит? Если, например, мы решили задачу для потока с одной скоростью V 1 и некоторого цилиндра диаметром D 1 а затем интересуемся обтеканием цилиндра другого диаметра D 2 другой жидкостью, то ноток будет одним и тем же при такой скорости V 2 , которая отвечает тому же самому числу Рейнольдса, т. е. когда
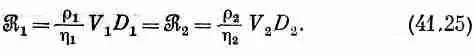
В любых случаях, когда числа Рейнольдса одинаковы, поток при выборе надлежащего масштаба х', у', z ' и t ' будет «выглядеть» одинаково. Это очень важное утверждение, ибо оно означает, что мы можем определить поведение потока воздуха при обтекании крыла самолета, не строя самого самолета и не испытывая его. Вместо этого мы можем сделать модель и провести измерения, используя скорость, которая дает то же самое число Рейнольдса. Именно этот принцип позволяет нам применять результаты измерений над маленькой моделью самолета в аэродинамической трубе или результаты, полученные с моделью корабля, к настоящим объектам. Напомню, однако, что это можно делать только при условии, что сжимаемостью жидкости можно пренебречь. В противном случае войдет новая величина — скорость звука. При этом различные модели будут действительно соответствовать друг другу только тогда, когда отношение V к скорости звука тоже приблизительно одинаково. Отношение скорости V к скорости звука называется числом Маха. Таким образом, для скоростей, близких к скорости звука или больших, поток в двух задачах будет выглядеть одинаково, если и число Маха и число Рейнольдса в обеих ситуациях одинаковы.
§ 4. Обтекание кругового цилиндра
Вернемся теперь обратно к задаче об обтекании цилиндра медленным (почти несжимаемым) потоком. Я дам вам качественное описание потока реальной жидкости. О таком потоке нам необходимо знать множество вещей. Например, какая увлекающая сила действует на цилиндр? Сила, увлекающая цилиндр, показана на фиг. 41.4 как функция величины 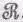 , которая пропорциональна скорости V , если все остальное фиксировано.
, которая пропорциональна скорости V , если все остальное фиксировано.
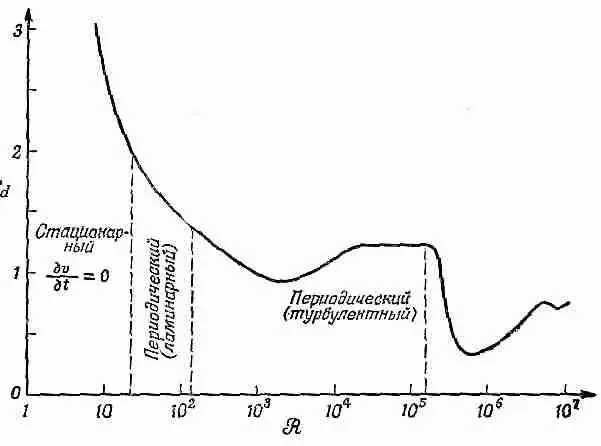
Фиг. 41.4. Коэффициент увлечения С d кругового цилиндра как функция числа Рейнольдса.
Фактически на рисунке отложен коэффициент увлечения С d — безразмерное число, равное отношению силы к 1 / 2 r V 2 Dl ( d — диаметр, l —длина цилиндра, а r —плотность жидкости):
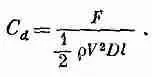
Коэффициент увлечения изменяется довольно сложным образом, как бы намекая нам на то, что в потоке происходит нечто интересное и сложное. Свойства потока полезно описывать для различных областей изменения числа Рейнольдса. Прежде всего, когда число Рейнольдса очень мало, поток вполне стационарен, скорость в любой точке потока постоянна и он плавно обтекает цилиндр. Однако распределение линий потока не похоже на их распределение в потенциальном потоке. Они описывают решение несколько другого уравнения. Когда скорость очень мала или, что эквивалентно, вязкость очень велика, так что вещество по своей консистенции напоминает мед, можно отбросить инерционные члены и описать поток уравнением
Читать дальше

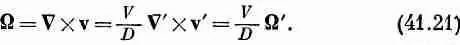
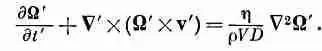
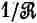 :
:
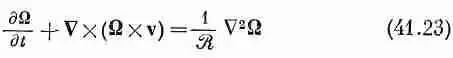
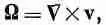
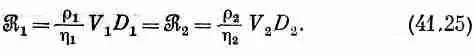
 , которая пропорциональна скорости V , если все остальное фиксировано.
, которая пропорциональна скорости V , если все остальное фиксировано.