Feynmann - Feynmann 7

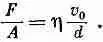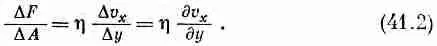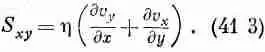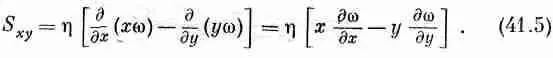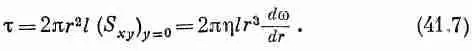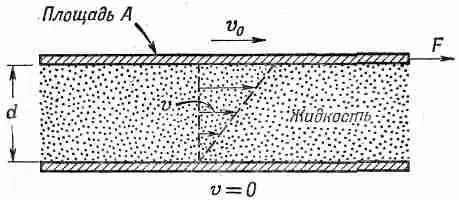
Фиг. 41.1. Увлечение жидкости между двумя параллельными пластинками.

Если вы будете измерять силу, требуемую для поддержания движения верхней пластины, то найдете, что она пропорциональна площади пластины и отно­шению v 0 / d , где d — расстояние между пластинами. Таким образом, напряжение сдвига F/A пропорционально v 0 /d:

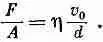
Коэффициент пропорциональности h называется коэффициен­том вязкости.

Если перед нами более сложный случай, то мы всегда можем рассмотреть в воде небольшой плоский прямоугольный объем, грани которого параллельны потоку (фиг. 41.2).

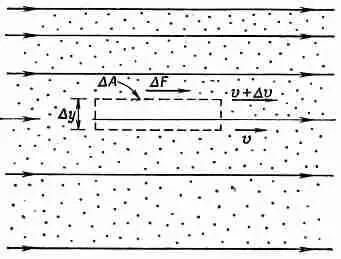
Фиг. 41.2. Напряжения сдви­га в вязкой жидкости.

Силы в этом объеме определяются выражением

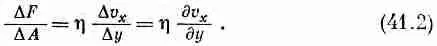
Далее, д v x / д y представляет скорость изменения деформаций сдвига, определенных нами в гл. 38, так что силы в жидкости пропорциональны скорости изменения деформаций сдвига.

В общем случае мы пишем

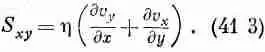
При равномерном вра­щении жидкости производ­ная д u х /ду равна д v y / д x с обратным знаком, a S xy будет равна нулю, как это и требуется, ибо в равно­мерно вращающейся жидкости напряжения отсутствуют. (Подобную же вещь мы проде­лывали в гл. 39 при определении е xy .) Разумеется, для S yz и S гх тоже есть соответствующие выражения.

В качестве примера применения этих идей рассмотрим дви­жение жидкости между двумя коаксиальными цилиндрами. Пусть радиус внутреннего цилиндра равен а, его скорость будет v а, а радиус внешнего цилиндра пусть будет b , а скорость равна v b (фиг. 41.3).

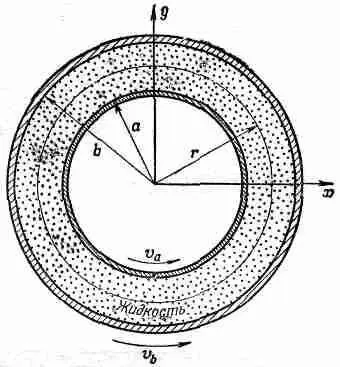
Фиг. 41 .3 . Поток жидкости между двумя концентрическими цилиндрами, вращающимися с разными угловыми скоростями.

Возникает вопрос, каково распределение скоростей между цилиндрами? Чтобы ответить на него, начнем с получения формулы для вязкого сдвига в жидкости на рас­стоянии r от оси. Из симметрии задачи можно предположить, что поток всегда тангенциален и что его величина зависит только от r ; v = v ( r ). Если мы понаблюдаем за соринкой в воде, расположенной на расстоянии r от оси, то ее координаты как функции времени будут

x = rcos w t, у = r sinwt,

где w= v / r . При этом х- и y-компоненты скорости равны

v x =- rwsinwt =-w у и v y = rwcoswt=w х. (41.4)

Из формулы (41.3) получаем

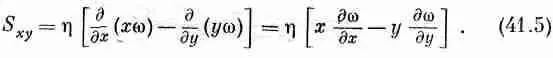
Для точек с у= 0 имеем д w /ду =0, а х(д w /дх) будет равно r ( d w )/ dr ). Так что в этих точках

(Разумно думать, что величина S должна зависеть от д w /д r , когда w не изменяется с r, жидкость находится в состоянии равномерного вращения и напряжения в ней не возникают.) Вычисленное нами напряжение представляет собой танген­циальный сдвиг, одинаковый повсюду вокруг цилиндра. Мы можем получить момент сил, действующий на цилиндриче­ской поверхности радиусом r, путем умножения напряжения сдвига на плечо импульса r и площадь 2 p rl :

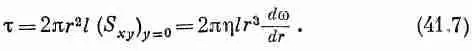
Поскольку движение воды стационарно и угловое уско­рение отсутствует, то полный момент, действующий на ци­линдрическую поверхность воды между радиусами r и r+ dr , должен быть нулем; иначе говоря, момент сил на расстоянии r должен уравновешиваться равным ему и противоположно на­правленным моментом сил на расстоянии r+ dr , так что t не должно зависеть от r . Другими словами, r 3(dw/dr) равно некоторой постоянной, скажем А, и