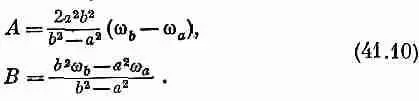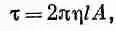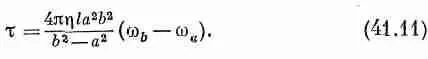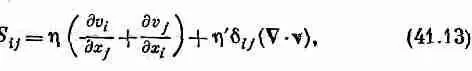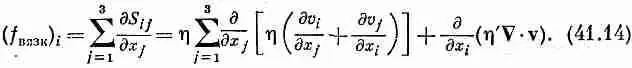Feynmann - Feynmann 7

dw/dr=A/r 3(41.8)

Интегрируя, находим как w изменяется с r:

Постоянные А и В должны определяться из условия, что w=w aв точке r = a , a w=w bв точке r = b . Тогда находим

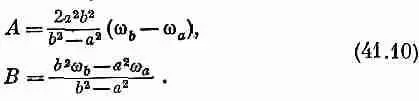
Таким образом, w как функция r нам известна, а стало быть, известно и v = w r .

Если же нам нужно определить момент сил, то его можно получить из выражений (41.7) и (41.8);

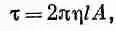
или

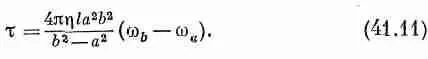
Он пропорционален относительной угловой скорости двух цилиндров. Имеется стандартный прибор для измерения коэф­фициентов вязкости, который устроен следующим образом: один из цилиндров (скажем, внешний) посажен на ось, но удер­живается в неподвижном состоянии пружинным динамометром, который измеряет действующий на него момент сил, а внутрен­ний цилиндр вращается с постоянной угловой скоростью. Коэффициент вязкости определяется при этом из формулы (41.11).

Из определения коэффициента вязкости вы видите, что h измеряется в ньютон · сек / м 2 . Для воды при 20° С

h=10 3 нъютон · сек/м 2 .

Часто удобнее бывает пользоваться удельной вязкостью, которая равна h, деленной на плотность r. При этом величины удельных вязкостей воды и воздуха сравнимы:

Вода при 20°С h/r=10 - 6 м 2 /сек

Воздух при 20°С h/r=15·10 - 6м 2/сек. , (41.12)

Обычно вязкость очень сильно зависит от температуры. Напри­мер, для воды непосредственно над точкой замерзания отно­шение h/r в 1,8 больше, чем при 20° С.

§ 2. Вязкий поток

Перейдем теперь к общей теории вязкого потока, по крайней мере настолько общей, насколько это и известно человеку. Вы уже понимаете, что компоненты сдвиговых напряжений сдвига пропорциональны пространственным производным от раз­личных компонент скорости, таких, как dv x / dy или dv y /дх. Однако в общем случае сжимаемой жидкости в напряжениях есть и другой член, который зависит от других производных скорости. Общее выражение имеет вид

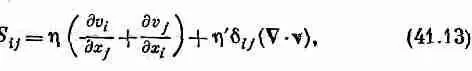
где х i — какая-либо из координат х, у или z ; v i — какая-либо з прямоугольных составляющих скорости. (Значок d ijобозна­чает символ Кронекера, который равен единице при i = j и нулю при i № j .) Ко всем диагональным элементам S ij тензора напряжений прибавляется дополнительный член h'С·v. Если жидкость несжимаема, то С·v=0 и дополнительного члена не появляется, так что он действительно имеет отношение к внутренним силам при сжатии. Для описания жидкости, точно так же как и для описания однородного упругого тела, требуются две постоянные. Коэффициент h представляет «обыч­ный» коэффициент вязкости, который мы уже учитывали. Он называется также первым коэффициентом вязкости, а новый коэффициент h' называется вторым коэффициентом вязкости.

Теперь нам предстоит найти вязкую силу f вязк, действую­щую на единицу объема, после чего мы сможем подставить ее в уравнение (41.1) и получить уравнение движения реальной жидкости. Сила, действующая на маленький кубический объем жидкости, представляет собой равнодействующую всех сил, действующих на все шесть граней. Взяв их по две сразу, мы получим разность, которая зависит от производных напряжений, и, следовательно, от вторых производных скоростей. Это прият­ный результат, ибо он приведет нас опять к векторному урав­нению. Компонента вязкой силы, действующей на единицу объема в направлении оси х i , равна

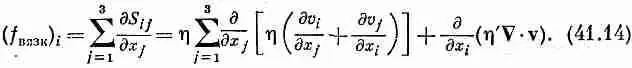
Обычно зависимость коэффициентов вязкости от координат положения несущественна и ею можно пренебречь. Тогда вяз­кая сила на единицу объема содержит только вторые производ­ные скорости. Мы видели в гл. 39, что наиболее общей формой вторых производных в векторном уравнении будет сумма Лапласиана (С·С)v = С 2v и градиента дивергенции (С (С·v)). Выражение (41.14) представляет как раз такую сумму с коэф­фициентами h и ( h+h'). Мы получаем