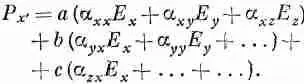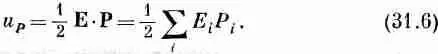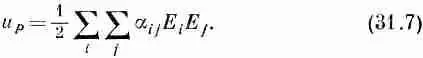Feynmann - Feynmann 7

Р x ’ =аР х + b Р у +сР z ,

и аналогично для других компонент. Если вместо Р х , Р y и Р z подставить их выражения через Е согласно (31.4), то получится

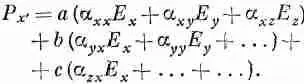
Теперь напишите, как выражается Е х , Е y и E z через Е x ' , Е y ' и Е z ' , например,

E x = a ' E x ' + b ' E y ' + c ' E z ' ,

где числа а' , b ' и с' связаны с числами а, b и c , но не равны им. Таким образом, у вас получилось выражение Р х ' через компо­ненты Е х ', Е y ' и E z ' , т. е. получились новые a ij. Никаких хит­ростей здесь нет, хотя все это достаточно запутано.

Когда мы говорили о преобразовании осей, то считали, что положение самого кристалла фиксировано в пространстве. Если же вместе с осями поворачивать и кристалл, то a не изме­няются. И обратно, если по отношению к осям изменять ориен­тацию кристалла, то получится новый набор коэффициентов а. Но если они известны для какой-то одной ориентации кристал­ла, то с помощью только что описанного преобразования их можно найти и для любой другой ориентации. Иначе говоря, диэлектрические свойства кристалла полностью описываются заданием компонент тензора поляризуемости a ij. в любой про­извольно выбранной системе координат. Точно так же как век­тор скорости v = (v x, v y , v z ) можно связать с частицей, зная, что три его компоненты при замене осей координат будут изменять­ся некоторым определенным образом, тензор поляризуемости a ij, девять компонент которого при изменении системы осей координат преобразуются вполне определенным образом, мож­но связать с кристаллом.

Связь между Ри Ев уравнении (31.4) можно записать в бо­лее компактном виде:

где под значком i понимается какая-то из трех букв х, у или z, а суммирование ведется по j = x , у и z. Для работы с тензорами было придумано много специальных обозначений, но каждое из них удобно для ограниченного класса проблем. Одно из та­ких общих соглашений состоит в том, что можно не писать знака суммы (S) в уравнении (31.5), понимая при этом, что когда один и тот же индекс встречается дважды (в нашем случае j ), то нужно просуммировать по всем значениям этого индекса. Однако, поскольку работать с тензорами нам придется немного, давайте не будем осложнять себе жизнь введением каких-то специальных обозначений или соглашений.

§ 3. Эллипсоид энергии

Потренируемся теперь в обращении с тензорами. Рассмот­рим такой интересный вопрос: какая энергия требуется для поляризации кристалла (в дополнение к энергии электрического поля, которая, как известно, равна e 0 Е 2 /2 на единицу объема)? Представьте на минуту атомные заряды, которые должны быть перемещены. Работа, требуемая для перемещения одного такого заряда на расстояние dx , равна qE x dx , а если таких зарядов в единице объема содержится N штук, то для перемещения их требуется работа qE x Ndx . Но qNdx равно изменению дипольного момента единицы объема dP x . Так что работа, затраченная на единицу объема, равна

E x dP x .

Складывая теперь работы всех трех компонент, найдем, ка­кой должна быть работа в единице объема:

E· d P .

Но поскольку величина Рпропорциональна Е, то работа, за­траченная на поляризацию единицы объема от 0 до Р, равна интегралу от E · d P . Обозначая ее через и р , можно написать

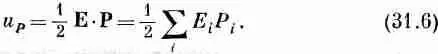
Теперь можно воспользоваться уравнением (31.5) и выра­зить Рчерез E .В результате получим

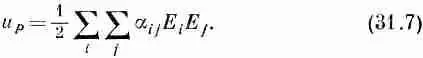
Плотность энергии и р — величина, не зависящая от выбора осей, т. е. скаляр. Таким образом, тензор обладает тем свойст­вом, что, будучи просуммирован по одному индексу (с векто­ром), он дает новый вектор, а будучи просуммирован по обоим индексам (с двумя векторами), дает скаляр.