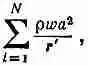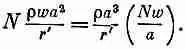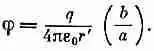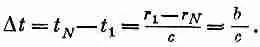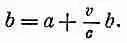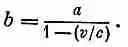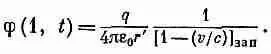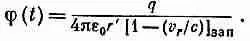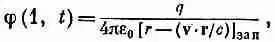Feynmann - Feynmann 6

Фиг. 21.6, Элемент объема D V i , используемый для вычисления потенциалов.

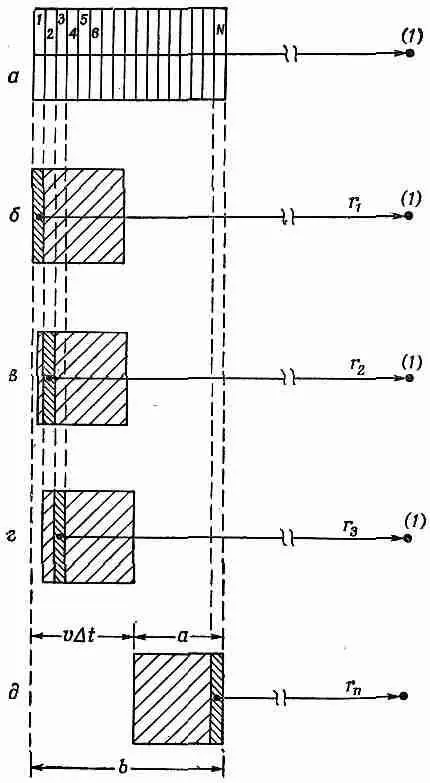
Фиг. 21.7. Интегрирование r ( t - r '/ c ) dV для движущегося заряда.

Тогда, вычисляя r 2DV 2, нужно взять положение заряда в несколько более позд­нее время t 2 =( t - r 2 / c ) и заряд к этому времени сместится в по­ложение, показанное на фиг. 21.7, в. Так же будет с DV 3, DV 4и т. д. Вот теперь можно подсчитывать сумму.

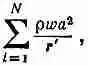
Толщина каждого DV i- равна w , а объем wa 2. Поэтому каж­дый элемент объема, накладывающийся на распределение заряда, содержит в себе заряд wa 2r, где r — плотность заряда внутри куба (мы считаем ее однородной). Когда расстояние от заряда до точки (1) велико, то можно все r iв знаменателях по­ложить равными некоторому среднему значению, скажем, взятому с учетом запаздывания положению r ' центра куба. Сумма (21.30) превращается в

где DV N—тот последний элемент DV i, который еще накла­дывается на распределение зарядов (см. фиг. 21.7, д). Сумма тем самым равна

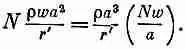
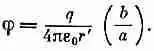
Но ra 3— просто общий заряд q , a Nw — длина b , показанная на фиг. 21.7, д. Получается

(21.31)

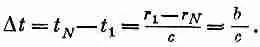
А чему же равно b? Это длина куба зарядов, увеличенная на расстояние, пройденное зарядом за время от t 1 =( t - r 1 /с) до t N =( t — r N /с). Это расстояние, пройденное зарядом за время

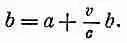
А поскольку скорость заряда равна v , то пройденное рас­стояние равно v D t = vb / c . Но длина b — само это расстояние плюс a:

Отсюда

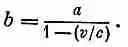
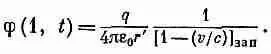
Здесь, конечно, под v подразумевается скорость в «запазды­вающий» момент t ' = ( t - r '/с); это можно указать, записав [1— v / c ] зап ; тогда уравнение (21.23) для потенциала прини­мает вид

Это согласуется с тем, что было предположено в (21.29). Поя­вился поправочный множитель. Он появился потому, что в то время, как наш интеграл «проносится над зарядом», сам заряд движется. Когда заряд движется к точке (1), его вклад в ин­теграл увеличивается в b /а раз. Поэтому правильное значение интеграла равно q / r ', умноженному на b /а, т.е. на 1/[1—v/c] з an.

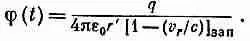
Если скорость заряда направлена не к точке наблюдения (1), то легко видеть, что важна только составляющая его скорости в направлении к точке (1). Если обозначить эту составляющую скорости через v r , то поправочный множитель запишется в виде 1/[1-v r/с] зап. Кроме того, проделанный нами анализ в равной степени проходит для распределения заряда любой формы (это не обязательно должен быть куб). Наконец, поскольку «раз­мер» а заряда не вошел в окончательный итог, то тот же резуль­тат получится, если заряд стянется до любых размеров, вплоть до точки. Общий результат состоит в том, что скалярный потен­циал точечного заряда, движущегося с произвольной скоростью,

(21.32)

Это уравнение часто пишут в эквивалентном виде:

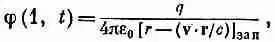
(21.33)

где r — вектор, соединяющий заряд с той точкой (1), в кото­рой вычисляется потенциал j, а все величины в скобках надо вычислять в «запаздывающий» момент времени t '=( t — r '/ c ).

То же самое получается и тогда, когда по (21.16) вычисляют А для точечного заряда. Плотность тока равна rv, а интеграл от r — тот же, что и в j. Векторный потенциал равен