Feynmann - Feynmann 6

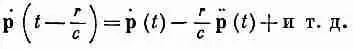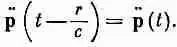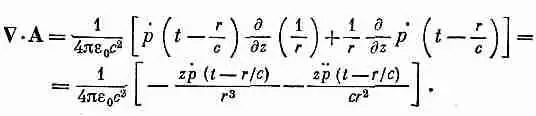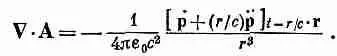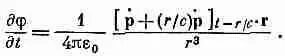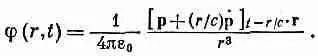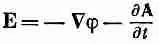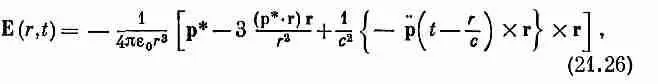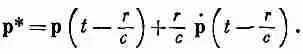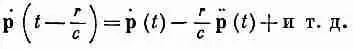
В этом можно убедиться следующим образом. Когда r мало, ( t - r /с) не очень отличается от t , и в (21.23) скобки можно раз­ложить в ряд Тэйлора. Первый член разложения дает

n в том же порядке по r /с

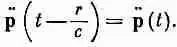
Если их сложить, члены с р уничтожатся и слева останется незапаздывающий ток р, т. е. р(t) плюс члены порядка (r/с) 2и выше [например, 1/ 2(r/с) 2Р"']. Эти члены при достаточно малых r (малых настолько, что за время r /с ток р заметно не меняется) будут очень малы.

Стало быть, (21.23) приводит к полям, очень похожим на те, которые дает теория с мгновенным действием, гораздо более по­хожим на них, чем на поля теории с мгновенным действием и с задержкой; эффекты задержки первого порядка компенсируют­ся вторым членом. Статические формулы очень точны, намного более точны, чем вам могло бы показаться. Конечно, компенса­ция чувствуется только вблизи от заряда. Для далеких точек эти поправки уже ничего не спасают, потому что временное за­паздывание приводит к очень большим эффектам и в конечном счете к важному члену 1/ r — к эффекту излучения.

Перед нами все еще стоит задача расчета электрического поля и доказательства того, что оно совпадает с (21.1'). Правда, уже чувствуется, что на больших расстояниях ответ получится такой, как надо. Мы знаем, что вдали от источников, где воз­никает распространяющаяся волна, Е перпендикулярно к В (и к r), как на фиг. 21.4, и что с В=Е. Значит, Е пропорциональ­но ускорению р", как и предсказывалось формулой (21.1').

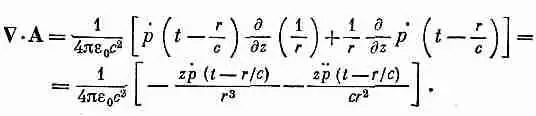
Чтобы получить электрическое поле на всех возможных рас­стояниях, нужно найти электростатический потенциал. Когда мы подсчитывали интеграл токов для А, желая получить (21.18), то сделали приближение: мы пренебрегли малозамет­ным изменением r в члене с запаздыванием. Для электростати­ческого потенциала этого делать нельзя, потому что тогда у нас получилось бы {/ r , умноженное на интеграл от плотности за­ряда, т. е. на константу. Такое приближение чересчур грубо. Надо обратиться к высшим порядкам. И вместо того, чтобы пу­таться в этих прямых расчетах высших приближений, можно поступить иначе — определить скалярный потенциал из равен­ства (21.6), используя уже найденное значение векторного по­тенциала. Дивергенция А в этом случае просто равна dAJdz , поскольку А х и A y тождественно равны нулю. Дифференцируя точно так же, как это делалось выше при вычислении В, получаем

Или в векторных обозначениях

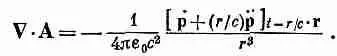
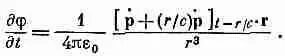
Из равенства (21.6) получается уравнение для j:

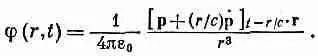
Интегрирование по t просто убирает надо всеми р по одной точке:

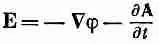
(Постоянная интегрирования отвечала бы некому наложенному статическому полю, которое, конечно, может существовать, но мы считаем, что у выбранного нами колеблющегося диполя ста­тического поля нет.) Теперь мы можем из

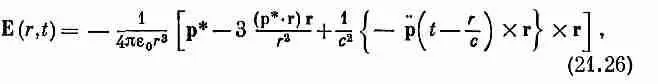
найти электрическое поле Е. После утомительных (хоть и пря­мых) выкладок [при этом нужно помнить, что p ( t - r /с) и его производные по времени зависят от х, у и z через запаздывание r /с] мы получаем

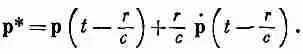
где

(21.27)

Это выглядит довольно сложно, но интерпретируется просто. Вектор р* — это дипольный момент с запаздыванием и с «по­правкой» на запаздывание, так что два члена с р* в (21.26) при малых r дают просто статическое поле диполя [см. гл. 6 (вып. 5), выражение (6.14)]. Когда r велико, то член с р преобладает над остальными, и электрическое поле пропорционально ускорению зарядов в направлении поперек r и само направлено вдоль