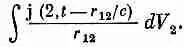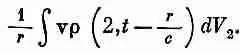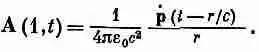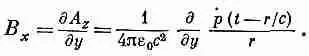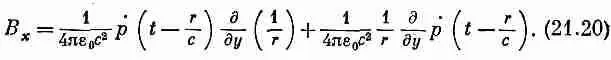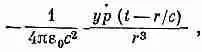Feynmann - Feynmann 6

Рассмотрим такую ситуацию, когда имеется сгусток заря­дов, каким-то образом перемещающийся в небольшой обла­сти; требуется найти создаваемые им где-то вдалеке от этого места поля.

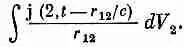
Можно поставить вопрос и иначе: мы найдем поле на произвольном расстоянии от точечного заряда, который почти незаметно колеблется вверх и вниз. Поскольку свет обычно испускают такие нейтральные тела, как атомы, то мы будем считать, что наш колеблющийся заряд q расположен вблизи неподвижного, равного по величине, но противоположного по знаку заряда. Если расстояние между центрами зарядов рав­но d, то у зарядов появится дипольный момент p = qd ,который мы будем считать функцией времени. Следует ожидать, что поблизости от зарядов запаздыванием поля можно будет прене­бречь; электрическое поле будет в точности таким же, как и то, которое получалось раньше для электростатического диполя [но, конечно, с мгновенным дипольным моментом p ( t )]. Однако при большом удалении в формуле для поля должно появиться добавочное слагаемое, которое меняется как 1/r и зависит от того, каково ускорение заряда в направлении, поперечном к лучу зрения. Посмотрим, получится ли у нас этот результат. Начнем с вычисления векторного потенциала А при помощи (2.16). Пусть плотность зарядов в сгустке есть r(х, у, z ) и весь он движется все время со скоростью v. Тогда плотность тока j ( x , у, z) равна vr(x,y, z ). Удобно систему координат располо­жить так, чтобы ось z была направлена по v; тогда геометрия нашей задачи изобразится так, как показано на фиг. 21.2. Нас интересует интеграл

(21.17)

Если размеры заряда-сгустка на самом деле намного мень­ше, чем r 12, то r 12в знаменателе можно положить равным r (расстоянию от центра сгустка) и вынести r за знак интеграла. Кроме того, мы собираемся положить и в числителе r 12=r, хотя это и не совсем верно. А неверно это потому, что на самом деле, скажем, полагается брать j в верхней части сгустка совсем не в тот момент, когда в нижней, а немного в другое время.

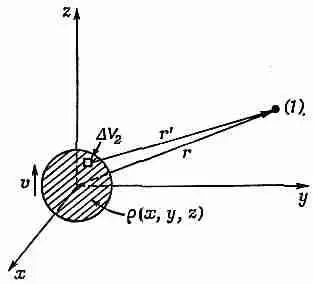
Фиг. 21.2. Потенциалы в точке (1) даются интегралами от плот­ности заряда r.

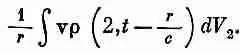
По­лагая r 12=r в j ( t - r 12/с), мы вычисляем плотность тока для всего сгустка в одно и то же время ( t - r /с). Это приближение годится лишь тогда, когда скорость v заряда много меньше с. Мы, стало быть, ведем расчет в нерелятивистском случае. После замены j на rv интеграл (21.17) превращается в

Раз скорость всех зарядов в сгустке одна и та же, этот инте­грал просто равен v/r, умноженному на общий заряд q . Но qv — это как раз dp / dt (скорость изменения дипольного момента), только надо ее, конечно, определять в более раннее время ( t - r /с). Запишем эту величину так: p ( t - r /с). Итак, мы полу­чаем для векторного потенциала

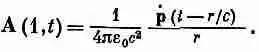
Мы узнали, что ток в меняющемся диполе создает векторный потенциал в форме сферических волн, источник которых обла­дает силой р’/4pe 0с 2.

Теперь из B=СXA можно получить магнитное поле. По­скольку р’ направлен по оси z , у А есть только z-компонента; в роторе остаются только две ненулевые производные. Значит, В х =дА г /ду и В =— дА z /дх. Поглядим сперва на В х :

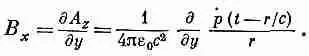
(21.19)

Чтобы продифференцировать, вспомним, что r=Ц(x: 2+y 2+z 2), так что

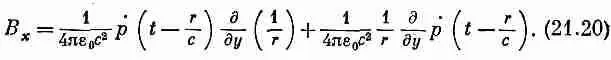
Но мы помним, что д r /ду = y / r ; значит, первое слагаемое даст

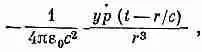
(21.21)

что убывает как 1/r 2, т. е. как поле статического диполя (потому что в данном направлении у/ r постоянно).