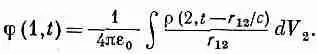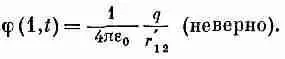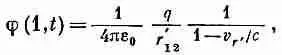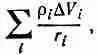Feynmann - Feynmann 6

проекции р на плоскость, перпендикулярную к r .

Этот результат согласуется с тем, что мы получили бы, применяя формулу (21.1'). Конечно, эта формула — более об­щая; она годится для любого движения, а не только для мало­заметных движений, для которых запаздывание r /с в пределах всего источника можно считать постоянным [как (21.26)]. Во всяком случае, теперь мы укрепили столбами все наше преж­нее изложение свойств света, за исключением лишь некоторых вопросов из гл. 34 (вып. 3), которые связаны с последней частью выражения (21.26). Мы можем теперь перейти к получению поля быстродвижущихся зарядов. Это приведет нас к релятивист­ским эффектам [гл. 34 (вып. 3)].

§5. Потенциалы движущегося заряда; общее решение Льенара и Вихерта

В предыдущем параграфе мы пошли на упрощение при вы­числении интеграла для А, рассматривая только небольшие скорости. Но при этом мы шли таким путем, которым легко можно прийти и к новым выводам. Поэтому сейчас мы заново предпри­мем расчет потенциалов точечного заряда, движущегося уже, как ему захочется (даже с релятивистской скоростью). Как только мы получим этот результат, у нас в руках окажутся электромагнитные свойства электрических зарядов во всей их полноте. Даже формулу (21.1') можно будет тогда легко полу­чить, взяв только нужные производные. И наш рассказ удастся, наконец, довести до конца. Итак, запаситесь терпе­нием!

Попробуем подсчитать в точке (х 1 , у 1 , z 1) скалярный по­тенциал j(1), создаваемый точечным зарядом (вроде электро­на), движущимся любым, каким угодно образом. Под «точеч­ным» зарядом подразумевается очень маленький заряженный шарик, такой маленький, как только можно себе представить, с плотностью заряда р(х, у, z ). Потенциал j можно найти из (21.15):

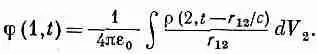
(21.28)

На первый взгляд кажется (и почти все так и подумают), что ответ состоит в том, что интеграл от r по такому «точечному» заряду равен просто общему заряду q , т. е. что

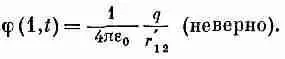
Через r ' 12 здесь обозначен радиус-вектор от заряда в точке (2) к точке (7), измеренный в более раннее время ( t — r 12 / c ). Эта формула ошибочна.

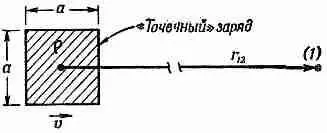
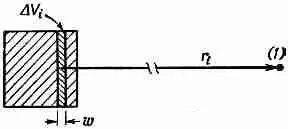
Фиг. 21.5. «Точечный» заряд (рассматриваемый как неболь­шое распределение зарядов в форме куба), движущийся со скоростью v к точке (1).

Правильный ответ такой:

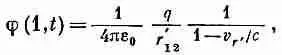
(21.29)

где v r ' — компонента скорости заряда, параллельная r 12, т. е. направленная к точке (1). Сейчас я объясню, почему это так. Чтобы легче было следить за моими доводами, я сперва проведу расчет для «точечного» заряда в форме небольшого заряженного кубика, который движется к точке (1) со ско­ростью v (фиг. 21:5). Сторона куба будет а, это число пусть будет много меньше r 12[расстояния от центра заряда до точки (1)].

Чтобы оценить величину интеграла (21.28), мы вернемся к основному определению: запишем его в виде суммы

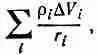
(21.30)

где r i — расстояние от точки (1) к i-му элементу объема DV i, а r i-— плотность заряда в DV iв момент t i =( t - r i /с). Поскольку все r i>> а, удобно будет выбрать все DV iв виде тонких прямо­угольных ломтиков, перпендикулярных к r 12(фиг. 21.6).

Предположим, что мы начали с того, что взяли элементы объема DV iнекоторой толщины w , много меньшей а.

Отдельные элементы объема будут выглядеть так, как по­казано на фиг. 21.7, а. Их нарисовано гораздо больше, чем нужно, чтобы закрыть весь заряд. А сам заряд не показан, и по весьма существенной причине. Где его нужно нарисовать? Ведь для каждого элемента объема DV iнадо брать r в свой момент t ~( t - r /с). Но раз заряд движется, то для каждого элемента объема DV i он окажется в другом месте !

Начнем, скажем, с элемента объема 1 на фиг. 21.7, а, выбранного так, чтобы в момент t l = ( t - r 1 /с) «задняя» грань заряда пришлась на DV i(фиг, 21.7, б).