Feynmann - Feynmann 6a

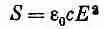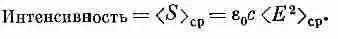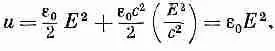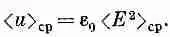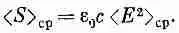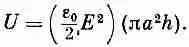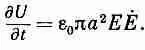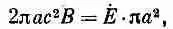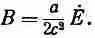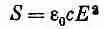
(27.16)

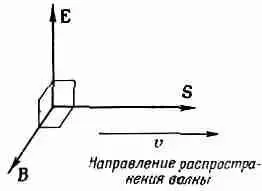
Фиг. 27.2. Векторы Е, В и S световой волны.

В световой волне, где E = E 0 cos w ( t - х/с), средняя скорость потока энергии через единичную площадь ср, которая на­зывается «интенсивностью» света, равна среднему значению электрического поля, помноженному на e а с:

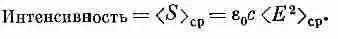
(27.17)

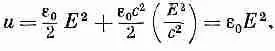
Этот результат, как ни странно, мы уже получали в гл. 31, § 5 (вып. 3), когда изучали свет. Мы получили его совсем другим путем и поэтому можем сейчас в него поверить. Когда у нас есть пучок света, то плотность энергии в пространстве задается урав­нением (27.14). Воспользовавшись теперь тем, что в световой волне сВ=Е, получаем

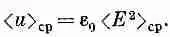
Однако вектор Е изменяется в пространстве, поэтому средняя плотность энергии равна

(27.18)

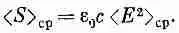
Далее, свет распространяется со скоростью с, поэтому можно думать, что энергия, проходящая в секунду через квадратный метр, равна произведению с на количество энергии в кубическом метре, т. е.

Все в порядке. Мы снова получили выражение (27.17).

Возьмем теперь другой пример, на этот раз очень любопыт­ный. Рассмотрим поток энергии в медленно заряжающемся кон­денсаторе. (Мы не хотим сейчас иметь дело со столь высокими ча­стотами, при которых конденсатор становится похожим на резо­нансную полость, но нам не нужен и постоянный ток.) Возьмем обычный конденсатор с круглыми параллельными пластинами (фиг. 27.3). Между ними создается почти однородное электри­ческое поле, которое изменяется с течением времени. Полная электромагнитная энергия внутри конденсатора в любой момент равна произведению плотности энергии и на объем. Если радиус пластин равен а, а расстояние между ними h , то полная энергия, заключенная между пластинами, будет

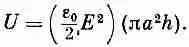
(27.19)

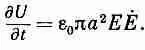
С изменением напряженности Е эта энергия тоже меняется. Когда конденсатор заряжается, внутренний объем приобретает энергию со скоростью

(27.20)

Так что должен существовать поток энергии, направленный откуда-то со стороны внутрь объема. Вы, конечно, думаете, что он идет от проводов, заряжающих конденсатор,— а вот и нет! Поток внутрь никоим образом не может идти с этой стороны, так как Е перпендикулярно к пластинам, а поэтому ЕXВ должно быть параллельно им.

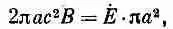
Вы, вероятно, помните, что при зарядке конденсатора воз­никает магнитное поле, которое направлено по окружности вокруг оси. Об этом говорилось в гл. 23. Воспользовавшись последним уравнением Максвелла, мы там нашли, что магнитное поле на краю конденсатора определяется выражением

или

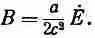
Направление его показано на фиг. 27.3. Таким образом, на краях конденсатора, как видно из рисунка, возникает поток энергии, пропорциональный ЕXВ. Так что энергия на самом деле втекает в конденсатор не со стороны проводов, а со стороны окружаю­щего его пространства.

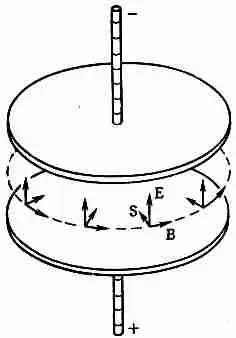
Фиг. 27.3. Вблизи заряженного конденсатора вектор Пойнтинга S направлен внутрь него

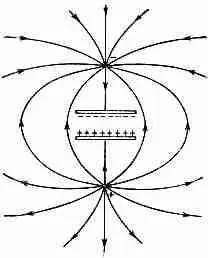
Фиг. 27.4. Поле вне конденсатора, заряженного двумя очень удален­ными зарядами.

Давайте проверим, согласуется ли полный поток через всю поверхность между краями пластин со скоростью изменения внутренней энергии. Для этого лучше всего повторить весь путь, проделанный нами при выводе выражения (27.15). Посмотрим, к чему он приведет. Площадь поверхности равна 2 p ah , а абсолютная величина S=e 0c 2(EXB) равна