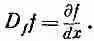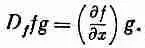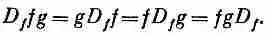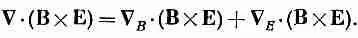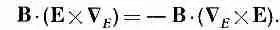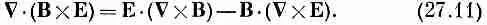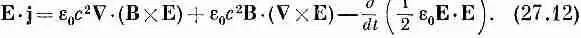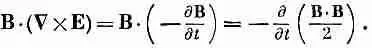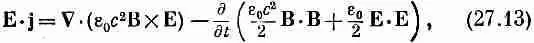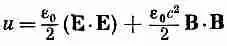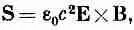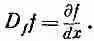
Но если мы имеем выражение D f fg , то оно означает
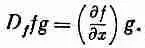
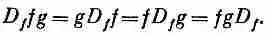
Заметим теперь, что, согласно нашему новому правилу, fD f g означает то же самое. Одно и то же выражение можно записать любым из следующих способов:
Вы видите, что D f может стоять даже после всего. (Странно, почему такому удобному обозначению обычно не учат в книгах по математике и физике.)
Вы, пожалуй, удивитесь: а что, если я хочу написать производную от fg ? Если мне нужна производная от обоих членов? Это очень легко: вы пишете D f ( fg ) + D g ( fg ), т.e. g ( df / dx ) + f ( dg / dx ), что в старых обозначениях как раз равно d ( fg )/ dx .
Вы сейчас увидите, как просто теперь получить новое выражение для С·(ВXЕ). Начнем с перехода к новому обозначению и напишем
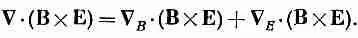
(27.10)
Как только мы сделали это, уже нет больше нужды придерживаться строгого порядка. Мы всегда знаем, что С Eдействует только на Е, a С Bдействует только на В. При этих обстоятельствах оператором С можно пользоваться как обычным вектором. (Разумеется, после того как все будет окончено, нам захочется вернуться к «стандартным» обозначениям, которые обычно используются.) Таким образом, теперь мы можем делать различные перестановки сомножителей. Так, средний сомножитель в уравнении (27.10) можно переписать как Е·(С BXВ). [Надеюсь, вы помните, что a·(bXc) = b·(cXa).] А последний — как В·(EXС E). Хотя это выглядит несколько странно, но тем не менее здесь все в порядке. Если же мы теперь попытаемся вернуться к старым обозначениям, то должны будем расположить операторы С так, чтобы они действовали на свои «собственные» переменные. В первом из них все в порядке, так что мы можем просто опустить индекс у С. Второй же требует некоторой реорганизации, чтобы оператор С поставить перед Е. Этого можно
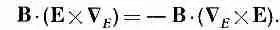
добиться, переставляя сомножители в векторном произведении и меняя знак:
Теперь все стоит на своем месте и можно вернуться к обычным обозначениям. Формула (27.10) эквивалентна следующему равенству:
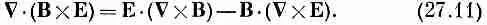
(В этом специальном случае быстрее было бы использовать компоненты, но, право же, стоило потратить время ради того, чтобы показать вам математический трюк. Может случиться, что вы больше нигде его не встретите, а он очень удобен тогда, когда в векторной алгебре нужно освободиться от правила порядка членов при дифференцировании.)
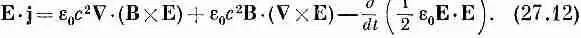
Вернемся теперь к нашему закону сохранения энергии, причем для преобразования СXB в (27.7) мы используем новый результат — равенство (27.11). Вот что оно дает:
Теперь вы видите, что мы почти у цели. Одно из наших слагаемых — настоящая производная no t , ее мы используем при образовании и, а другое (превосходная дивергенция) войдет в S. К несчастью, справа в середине осталось еще одно слагаемое, которое не является ни дивергенцией, ни производной по t . Так что пока еще не все закончено. После некоторых размышлений мы опять обращаемся к уравнениям Максвелла и, к счастью, обнаруживаем, что (СXE) равно — dB / dt .
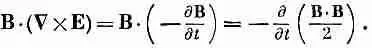
Это позволяет превратить дополнительный член в чистую производную чего-то по времени:
Вот теперь у вас получилось то, что нужно. Уравнение для энергии переписывается в виде
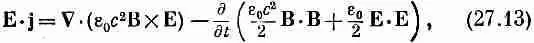
А это, если мы определим u и S как
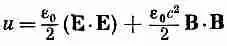
(27.14)
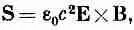
Читать дальше