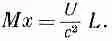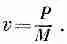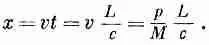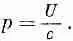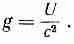Feynmann - Feynmann 6a

Наконец, я приведу рассуждение Эйнштейна, которое еще раз продемонстрирует то же самое утверждение. Предположим, у нас есть вагон с какой-то большой массой М, который может без трения катиться по рельсам. В одном его конце расположено устройство, способное «выстреливать» какие-то частицы или световой импульс (совершенно безразлично, чем оно стреляет), которые ударяются о противоположный конец вагона. Следо­вательно, некоторое количество энергии, скажем U , находив­шееся первоначально на одном конце (фиг. 27.7,а), перелетает на противоположный конец (фиг. 27.7,в). Таким образом, энергия U перемещается на расстояние, равное длине вагона L . Этой энергии U соответствует масса U/с 2, так что если вагон вначале стоял, то его центр масс должен передвинуться. Эйнштейну не понравилось заключение о том, что центр масс предмета можно переместить какими-то манипуляциями внутри него. Он считал, что никакие внутренние действия не могут изменить центр масс. Но если это так, то при перемещении энергии U с одного конца на другой сам вагон должен откатиться на расстояние х

(фиг. 27.7, в). В самом деле, нетрудно убедиться, что полная масса вагона, умноженная на х, должна быть равна произведе­нию перемещенной энергии U / c 2 на длину L (при условии, что U / C 2 много меньше М), т. е.

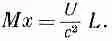
(27.22)

Теперь рассмотрим конкретный случай, когда энергия пере­носится вспышкой света. (Все рассуждения можно повторить и для частиц, но мы будем следовать за Эйнштейном, который интересовался проблемами света.) Что заставляет вагон дви­гаться? Эйнштейн рассуждал так: при испускании света должна быть отдача, какая-то неизвестная отдача с импульсом р. Именно она заставляет вагон откатиться назад. Скорость ва­гона v при такой отдаче должна быть равна импульсу отдачи, поделенному на массу М:

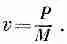
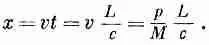
Вагон движется с этой скоростью до тех пор, пока свет не достигнет противоположного конца. Ударяясь, свет отдает импульс вагону и останавливает его. Если х мало, то время, в течение которого вагон движется, равно l/c, так что мы

Подставляя х в (27.22), находим

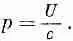
Снова получилось соотношение между энергией и импульсом света. Деля это на с, находим плотность импульса g = p / c , и опять

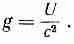
(27.23)

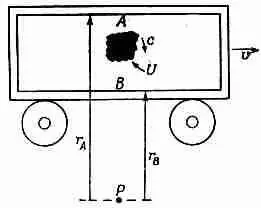
Вас может удивить, так ли уж важна теорема о центре масс. Может быть, она нарушается? Возможно, но тогда вы теряете и закон сохранения момента количества движения. Предполо­жим, что наш вагончик движется по рельсам с некоторой ско­ростью и, и мы «выстреливаем» какое-то количество световой энергии от потолка к полу, например из точки А в точку В (фиг. 27.8). Посмотрим теперь на момент количества движения относительно точки Р. До того как порция энергии U покинула точку А, у нее была масса m = U 2 / c и скорость v , так что ее мо­мент количества движения был равен mvr a . Когда же она приле­тела в точку В, масса ее остается прежней, и если импульс всего вагона не изменился, то она по-прежнему должна иметь скорость v .

Фиг. 27 .8. Для сохранения мо­мента количества движения отно­сительно точки Р порция энергии U должна нести импульс U / c .

Однако момент количества движения относительно точки Р будет уже mvr B . Таким образом, если вагону при излу­чении света не передается никакого импульса, т. е. если свет не переносит импульса U / c , то момент количества движения должен измениться. Оказывается, что в теории относительности сохранение момента количества движения и теорема о центре масс тесно связаны между собой. И если неверна теорема, то нарушается и закон сохранения момента количества движения. Во всяком случае, общий закон должен быть справедлив и для электродинамики, так что им можно воспользоваться для полу­чения импульса поля.