Feynmann - Feynmann 6a

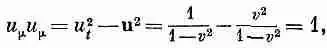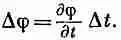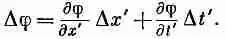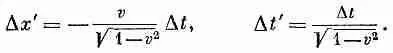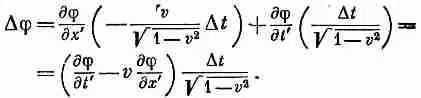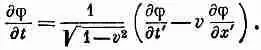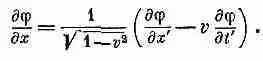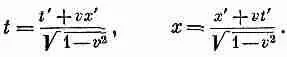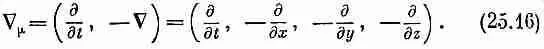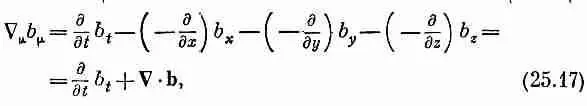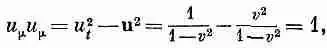
Скалярное произведение — инвариант, поэтому полезно знать его величину. Что, например, можно сказать о «длине» четырехвектора скорости u mu m?

т. е. u m — единичный четырехвектор.

§ 3. Четырехмерный градиент

Следующей величиной, которую нам следует обсудить, яв­ляется четырехмерный аналог градиента. Напомним (см. гл. 14, вып. 1), что три оператора дифференцирования д/дх, д/ду, d / dz преобразуются подобно трехмерному вектору и назы­ваются градиентом. Та же схема должна работать и в четырех измерениях; по простоте вы можете подумать, что четырехмер­ным градиентом должны быть ( d / dt , д/дх, д/ду d / dz ), но это неверно.

Чтобы обнаружить ошибку, рассмотрим скалярную функ­цию, которая зависит только от х и t . Приращение j при малом изменении t на Dt и постоянном х равно

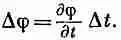
(25.13)

С другой стороны, с точки зрения движущегося наблюда­теля

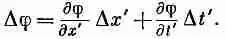
Используя уравнение (25.1), мы можем выразить D х' и D t ' через D t . Вспоминая теперь, что величина х постоянна, так

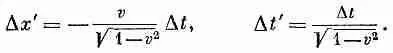
что Dx=0, мы пишем

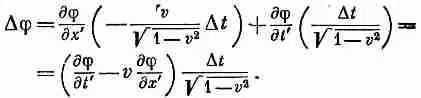
Таким образом,

Сравнивая этот результат с (25.13), мы узнаем, что

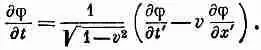
(25.14)

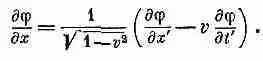
Аналогичные вычисления дают

(25.15)

Теперь вы видите, что градиент получился довольно странным. Выражения для х и t через х' и t ' [полученные решением уравнений (25.1)] имеют вид

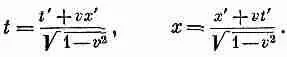
Именно так должен преобразовываться четырехвектор. Но в уравнениях (25.14) и (25.15) знаки получились неправильными! Выход в том, что надо заменить неправильное определение четырехмерного оператора градиента ( d / dt , С) правильным:

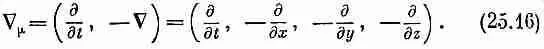
Мы его обозначим С m. Для такого С mтрудности исчезают, и он ведет себя так, как подобает настоящему четырехвектору. (Ужасно неприятно наличие минусов, но так уж устроено в мире.) Разумеется, говоря, что С m«ведет себя как четырехвектор», мы подразумеваем, что четырехмерный градиент ска­лярной функции есть четырехвектор. Если j — настоящее ска­лярное (лоренц-инвариантное) поле, то С mj будет четырехвекторным полем.

Итак, все уладилось. Теперь у нас есть векторы, градиенты и скалярное произведение. Следующий на очереди — инвари­ант, аналогичный дивергенции в трехмерном векторном ана­лизе. Ясно, что аналогом его должно быть выражение С mb m, где b m — векторное поле, компоненты которого являются функ­циями пространства и времени. Мы определим дивергенцию четырехвектора b m =( b t , b) как скалярное произведение С mна b m:

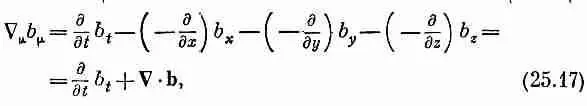
где С·b — обычная трехмерная дивергенция вектора b. Не забы­вайте внимательно следить за знаками. Один знак минус свя­зан с определением скалярного произведения [формула (25.7)1, а другой возникает от пространственных компонент С m[форму­ла (25.16)]. Дивергенция, определяемая формулой (25.7), есть инвариант, и для всех систем координат, отличающихся друг от друга преобразованием Лоренца, применение ее приводит к одинаковой величине.

Остановимся теперь на физическом примере, в котором появ­ляется четырехмерная дивергенция. Ею можно воспользоваться при решении задачи о полях вокруг движущегося проводника. Мы уже видели (гл. 13, § 7, вып. 5), что плотность электрического заряда r и плотность тока j образуют четырехвектор j m = ( p , j ). Если незаряженный провод переносит ток j x , то в системе от­счета, движущейся относительно него со скоростью v (вдоль оси х), в проводнике наряду с током появится и заряд [который возникает согласно закону