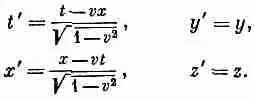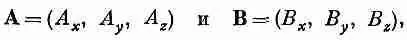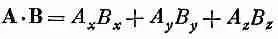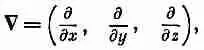Feynmann - Feynmann 6a

2 В нашем случае это произойдет при l 0 < 2 / 3 а. Но вообще-то это может происходить и при l 0<���а. Эти добавочные волны отве­чают высшим типам волн, о которых мы говорили.

После нашего анализа становится также ясно, отчего фазо­вая скорость волн, бегущих по трубе, превышает с и зависит от со. Когда w меняется, меняется и угол на фиг. 24.16, под ко­торым в пустом пространстве распространяются волны, а вместе с этим меняется и скорость вдоль трубы.

Хотя мы описали волны в волноводе в виде суперпозиции по­лей бесконечной совокупности линейных источников, но можно убедиться в том, что тот же результат можно было бы получить, представив себе две совокупности волн в пустом пространстве, многократно отражаемых от двух идеальных зеркал вперед и назад, и вспоминая, что подобное отражение означает перемену знака фазы. Эти совокупности отражаемых волн гасили бы друг друга под всеми углами, кроме угла q [см. (24.33)]. Одну и ту же вещь можно рассматривать многими способами.

Глава 25

ЭЛЕКТРОДИНАМИКА

В РЕЛЯТИВИСТСКИХ ОБОЗНАЧЕНИЯХ

§ 1. Четырехвекторы

§ 2. Скалярное произведение

§ 3. Четырехмерный градиент

§ 4. Электродинамика в четырехмерных обозначениях

§ 5. Четырехмерный потенциал движущегося заряда

§ 6. Инвариантность уравнений электродинамики

В этой главе с=1

Повторить: гл. 15 (вып. 2) «Специ­альная теория от­носительности» ; гл. 16 (вып. 2) «Релятивистская энергия и им­пульс»;

гл. 17 (вып. 2} «Пространство - время»; гл. 13 (вып. 5) «Магнитостатика»

§ 1 . Четырехвекторы

В этой главе мы рассмотрим применение спе­циальной теории относительности к электроди­намике. Мы изучали теорию относительности довольно давно (гл. 15—17, вып. 2), поэтому я здесь коротко напомню основные идеи.

Экспериментально установлено, что законы физики при равномерном движении не изме­няются. Если вы находитесь внутри звездо­лета, летящего с постоянной скоростью по пря­мой линии, то не можете установить самого фак­та движения корабля: для этого надо выглянуть наружу или по крайней мере провести какие-то наблюдения, связанные с внешним миром. Лю­бой написанный нами истинный закон физики должен быть сформулирован так, чтобы этот факт природы был «встроен» в него.

Соотношение между пространством и време­нем в двух системах координат (одна из которых 6" равномерно движется относительно другой 5 в направлении оси х со скоростью v ) опреде­ляется преобразованиями Лоренца

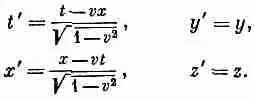
(25.1)

Законы физики должны быть таковы, чтобы после преобразований Лоренца они в новой фор­ме выглядели абсолютно так же, как и раньше. Это в точности напоминает принцип независи­мости законов физики от ориентации нашей системы координат. В гл. 11 (вып. 1) мы видели, что способом математического описания этой инвариантности относительно вращения являет­ся запись уравнений в векторном виде.

Там мы обнаружили, что если, скажем, взять два вектора

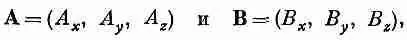
то комбинация

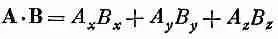
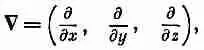
при повороте системы координат не меняется. Таким образом, если с обеих сторон уравнения мы видим скалярное произведе­ние, подобное А·В, то уравнение будет иметь в точности ту же форму в любой повернутой системе координат. Кроме того, мы открыли оператор (см. гл. 2)

который, будучи применен к скалярной функции, дает три вели­чины, преобразующиеся в точности как вектор. С помощью это­го оператора был определен градиент, а в комбинации с дру­гими векторами — дивергенция и лапласиан. И, наконец, мы обнаружили, что, составляя суммы некоторых попарных произ­ведений компонент двух векторов, можно получить три вели­чины, которые ведут себя подобно новому вектору. Мы назвали это векторным произведением двух векторов. Используя затем векторное произведение с оператором V, мы определили ротор вектора. В дальнейшем нам часто придется ссылаться на то, что было нами сделано в векторном анализе, поэтому все важнейшие векторные операции в трехмерном пространстве, которые использовались в прошлом, мы собрали в табл. 25.1.