Feynmann - Feynmann 4

Т = D P / D T - P =0 (при постоянном V ), (45.11)

интегрирование не составит для нас труда, и мы получим ln P = ln Т +const (при постоянном V ),

P = const X T (при постоянном V ). (45.12)

Мы знаем, что давление идеального газа равно

Р= RT / V . (45.13)

Это соотношение совместимо с (45.12), потому что R и V — постоянные. Но зачем же мы мучились, решая эти уравнения? Ведь результат-то был уже известен. Потому что мы пользова­лись двумя независимыми определениями температуры! Однаж­ды мы предположили, что кинетическая энергия молекул про­порциональна температуре. Это предположение привело нас к температурной шкале, которую мы назвали шкалой идеаль­ного газа. Температура Т в уравнении (45.13) отсчитывается по газовой шкале. Мы называли отсчитанную по газовой шкале температуру кинетической температурой. Потом мы определили температуру иначе, и это определение вообще не нуждалось ни в каком веществе. Исходя из второго закона, мы определили то, что можно назвать «абсолютной термодинамической темпера­турой» Т; она появляется в уравнении (45.12). Здесь мы только доказали, что давление идеального газа (идеальный газ для нас нечто, чья внутренняя энергия не зависит от объема) пропор­ционально абсолютной термодинамической температуре. Мы, кроме того, знаем, что давление пропорционально температуре, измеренной по газовой шкале. Таким образом, можно заклю­чить, что кинетическая температура пропорциональна «абсо­лютной термодинамической температуре». Это, конечно, озна­чает, что если бы мы были благоразумны, то показания обеих шкал могли бы всегда жить в согласии. В конце концов эти шкалы можно выбрать так, что они совпадут; постоянную про­порциональности можно положить равной единице. Очень долго люди сами себе создавали трудности, но наконец прев­ратили две шкалы в одну!

§ 3. Уравнение Клаузиуса— Клайперона

Испарение жидкости — это еще одна область, в которой можно применить наши результаты. Предположим, что мы вдвигаем поршень в цилиндр с каким-то веществом.

Естественно задать себе вопрос: как зависит давление от объе­ма, если температура остается постоянной? Иначе говоря, мы хотим начертить изотермические линии на диаграмме Р— V . Вещество в цилиндре — это далеко не идеальный газ, с которым мы имели дело; теперь это жидкость или пар, а может быть, и то и другое вместе. Если сжать вещество достаточно сильно, то оно начнет превращаться в жидкость. Если мы будем увеличи­вать давление, объем изменится очень мало, а наши изотермы при уменьшении объема пойдут резко вверх, как это показано в левой части фиг. 45.3.

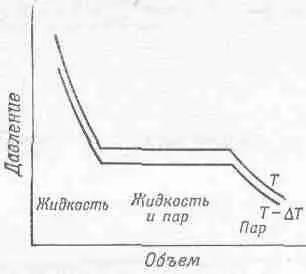
Фиг. 45.3. Изотермы конденси­рующегося пара.

Пар сжимается в цилиндре. Слева — все вещество превратилось в жидкость; справа — вся жидкость испарилась; в середине — в цилиндре сосуществуют жидкость и пар.

Если увеличивать объем, выдвигая поршень из цилиндра, давление будет падать, пока мы не достигнем точки кипения жидкости и в цилиндре появится пар. Дальнейшее вытягивание поршня приведет к более сильному испарению. Когда цилиндр заполнен частично паром, а частично жидкостью, то между ними устанавливается равновесие — жидкость испаряется, пар кон­денсируется, и скорости этих процессов равны. Если предоста­вить пару больший объем, то, чтобы удержать прежнее давле­ние, понадобится больше пара. Поэтому, хоть жидкость все испаряется, давление остается прежним. Вдоль плоской части кривой на фиг. 45.3 давление не изменяется, это давление назы­вается давлением пара при температуре Т. Если объем все увеличивается, наступит момент, когда запасы жидкости иссяк­нут. В такой ситуации давление падает при увеличении объема, ведь теперь мы имеем дело с обычным газом; это изображено в правой части диаграммы Р— V . Нижняя кривая на фиг. 45.3— это изотермическая кривая при более низкой температуре Т —D T . Давление жидкости в этом случае немного меньше, потому что с ростом температуры жидкости расширяются (не все жидкости, вода около точки замерзания поступает наоборот), а давление пара при уменьшении температуры, конечно, падает.

Из двух изотерм можно снова построить цикл, соединив концы их плоских участков (скажем, адиабатами), как это показано на фиг. 45.4. Небольшая зазубрина в нижнем правом углу фигуры несущественна, и мы просто забудем о ней. Исполь­зуем аргументы Карно, которые показывают, как связано тепло, подведенное к жидкости для превращения ее в пар, с работой, совершаемой веществом при обходе цикла. Пусть L—это тепло, необходимое для испарения жидкости в цилиндре. Вспом­ним, как мы рассуждали при выводе уравнения (45.5), и не­медленно скажем, что L ( D T / T ) равно работе, совершенной ве­ществом. Как и раньше, работа вещества равна площади, за­ключенной внутри цикла. Эта площадь приблизительно равна D P(V G— V L ), где D Р — разность давлений пара при температурах Т и Т— D T, V G — объем газа, a V L — объем жидкости. Оба объе­ма надо измерять при давлении, равном давлению пара.