Feynmann - Feynmann 4

Сформулируем пояснее наши аргументы. Мы убедились, что всегда можем связать тепло, поглощенное при температуре T 1 и тепло, выделенное при температуре T 2, определив тепло, выделенное при какой-то другой температуре T 3 . Это значит, что мы можем описать все свойства машины, если введем стан­дартную температуру и будем анализировать все процессы с помощью именно такой стандартной температуры. Иначе говоря, если мы знаем коэффициент полезного действия машины, рабо­тающей между температурой Т и какой-то стандартной темпе­ратурой, то сможем вычислить коэффициент полезного действия машины, работающей при любом перепаде температур. Ведь мы рассматриваем только обратимые машины, поэтому ничто не мешает нам спуститься от начальной температуры к стандарт­ной, а потом снова вернуться к конечной температуре. Примем температуру в один градус за стандартную. Для обозначения выделяемого при стандартной температуре тепла используем особый символ Q s . Это значит, что если машина поглощает при температуре Т тепло Q , то при температуре в один градус она выделяет тепло Q S . Если какая-то машина, поглощая тепло Q 1 при T 1 , выделяет тепло Q S при температуре в один градус, а другая машина, поглотив тепло Q 2 при Т 2 , выделяет то же самое тепло Q S при температуре в один градус, то машина, поглощающая Q 1 при Т 1 , должна при температуре Т 2 выделять тепло Q 2 . Мы уже доказали это, рассмотрев три машины, ра­ботающие при трех температурах. Таким образом, для полного описания работы машин нам остается узнать совсем немного. Мы должны выяснить, сколько тепла Q 1 должна поглотить ма­шина при температуре T 1 , чтобы выделить при единичной тем­пературе тепло Q S . Конечно, между теплом Q и температурой Т существует зависимость. Легко понять, что тепло должно воз­растать при возрастании температуры, ведь мы знаем, что если заставить работать машину в обратном направлении, то при более высокой температуре она отдает тепло. Легко также по­нять, что тепло Q 1должно быть пропорционально Q S . Таким образом, наш великий закон выглядит примерно так: Каждому количеству тепла Q S , выделенного при температуре в один градус, соответствует количество тепла, поглощенного машиной при температуре Т, равное Q S , умноженному на не­которую возрастающую функцию Q температуры:

Q = Q S f ( T ). (44.9)

§ 5. Термодинамическая температура

Пока мы не будем делать попыток выразить эту возрастаю­щую функцию в терминах делений знакомого нам ртутного гра­дусника, а взамен определим новую температурную шкалу. Когда-то «температура» определялась столь же произвольно. Мерой температуры служили метки, нанесенные на равных расстояниях на стенках трубочки, в которой при нагревании расширялась вода. Потом решили измерить температуру ртут­ным термометром и обнаружили, что градусные расстояния уже не одинаковы. Сейчас мы можем дать определение температуры, не зависящее от каких-либо частных свойств вещества. Для этого мы используем функцию f ( T ), которая не зависит ни от одного устройства, потому что эффективность обратимых машин не зависит от их рабочего вещества. Поскольку найденная нами функция возрастает с температурой, то мы можем считать, что она сама по себе измеряет температуру, начиная со стандартной температуры в один градус. Для этого надо только договориться, что

Q = Q S T , (44.10)

а

Q S = S · 1°. (44.11)

Это означает, что теперь мы можем найти температуру тела, определив количество тепла, которое поглощается обратимой машиной, работающей в интервале между температурой тела и температурой в один градус (фиг. 44.9)

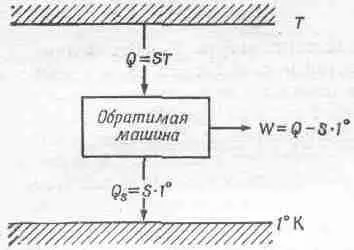
Фиг. 44.9. Абсолютная термо­динамическая температура.

Если машина забирает из котла в семь раз больше тепла, нежели поступает в одно­градусный конденсор, то температура котла равна семи граду­сам и т. д. Таким образом, измеряя количество тепла, погло­щаемого при разных температурах, мы определяем температуру. Полученная таким образом температура называется абсолютной термодинамической температурой и не зависит от свойств ве­щества. Теперь мы будем пользоваться исключительно этим определением температуры.