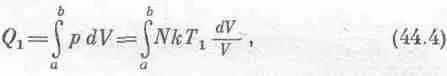Feynmann - Feynmann 4

Нам нужно лишь получить формулы для Q 1 и Q 2(ведь W = Q 1 - Q 2 ) — тепла, которым машина обменивается с резерву­арами во время изотермического расширения и сжатия. Для примера вычислим Q 1 — тепло, полученное от резервуара при температуре T 1во время изотермического расширения (кривая 1 на фиг. 44.6) от точки а, где давление равно p a , объем V a , тем­пература Т 1 , до точки b , где давление равно р b , объем V b , а тем­пература та же самая T 1 . Энергия каждой молекулы идеального газа зависит только от температуры, а поскольку в точках а и b одинаковы и температура, и число молекул, то и внутренняя энергия тоже одинакова. Энергия U не изменяется; полная рабо­та газа в период расширения

W = a b ∫ pdV

а

совершается за счет энергии Q 1 , полученной из резервуара. Во время расширения pV = NkT 1 или

p-NkT 1/V; значит,

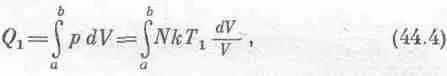
т. е.

Q 1 =NkT 1 ln(V b /V a ).

Вот то тепло, которое взято из резервуара при температуре Т 1 . Точно так же можно вычислить и тепло, отданное при сжатии (кривая 3 на фиг. 44.6) резервуару при температуре T 2 :

Q 2 = NkT 2 ln ( V c / V d ). (44.5)

Чтобы закончить анализ, нужно еще найти соотношение между V c / V d и V b / V a . Для этого взглянем сначала на кривую 2, которая описывает адиабатическое расширение от b до c . В это время pV g остается постоянным. Поскольку pV = NkT , то фор­мулу для адиабатического расширения в конечных точках пути можно записать в виде (pV)V g -1=const, или TV g -1=const, т. е.

T 1V b g -1=T 2V c g -1. (44.6)

Так как кривая 4 описывает адиабатическое сжатие от d до а, то

Т 1 V a g -1 = T 2 V d g -1 . (44.6а)

Если поделить эти равенства одно на другое, то мы выясним, что отношения V b / V a и V c / V d равны, поэтому равны и лога­рифмы в (44.4) и (44.5). Значит,

Q 1/T 1=Q 2/T 2. (44.7)

Это и есть то соотношение, которое мы искали. Хотя оно дока­зано для машины с идеальным газом, мы уже знаем, что оно справедливо для любой обратимой машины.

А теперь посмотрим, как можно вывести этот универсальный закон на основании только логических аргументов, не интере­суясь частными свойствами веществ. Предположим, что у нас есть три машины и три температуры Т 1 , Т 2 и Т 3 . Одна машина поглощает тепло Q 1 при температуре T 1, производит работу W 13 и отдает тепло Q 3 при температуре T 3 (фиг. 44.8).

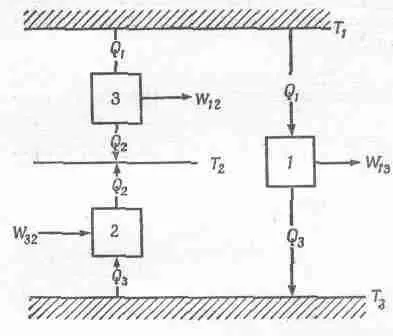
Фиг. 44.8. Спаренные машины 1 и 2 эквивалентны машине 3.

Другая машина работает при перепаде температур t 2 и Т 3 . Предположим, что эта машина устроена так, что она поглощает то же тепло Q 3 при температуре Т 3 и отдает тепло Q 2. Тогда нам придется затратить работу W 32, ведь мы заставили машину работать в обратном направлении. Цикл первой машины заклю­чается в поглощении тепла Q 1и выделении тепла Q 3 при тем­пературе Т 3 . Вторая машина в это время забирает из резер­вуара то же самое тепло Q 3 при температуре T 3 и отдает его в резервуар с температурой Т 2 . Таким образом, чистый резуль­тат цикла этих спаренных машин состоит в изъятии тепла Q l при температуре Т 1 и выделении тепла Q 2при температуре T 2. Эти машины эквивалентны третьей, которая поглощает тепло Q l при температуре Т 1 , совершает работу W 12 и выделяет тепло Q 2при температуре Т 2 . Действительно, исходя из первого за­кона, можно сразу же показать, что W 12=W 13- W 32 :

W 13 - W 32 =( Q 1 - Q 3 )=( Q 2 - Q 3 )= Q 1 - Q 2 = W 12 . (44.8)

Теперь можно получить закон, связывающий коэффициенты полезного действия машин. Ведь ясно, что между эффективностями машин, работающих при перепаде температур Т 2 - T 3 , t 2 - Т 3 и Т 1 - Т 2 , должны существовать определенные соотно­шения.