Feynmann - Feynmann 4

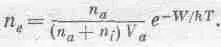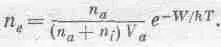
Эти равенства верны, и мы в конце концов всегда используем их при решении реальных задач. Но нам нужно получить другое соотношение между этими величинами. Сделать это можно так. Обратимся снова к идее о том, что для отрыва электрона от атома требуется какое-то количество энергии, которую мы будем называть энергией ионизации и обозначать буквой W (чтобы новые формулы выглядели так же, как и раньше). Итак, W равна энергии, потребной для того, чтобы оторвать электрон от атома и получить ион. Мы снова убеждаемся, что число свободных электронов в единичном объеме «пара» равно произведению числа электронов в единичном объеме, связан­ных в атомах, на е в степени минус разность энергий связанного и свободного электронов, деленная на kT . Опять основное уравнение. Но как это записать? Число свободных электронов в единичном объеме, конечно, n e , потому что определение n е. Ну, а что можно сказать о числе связанных в атоме элек­тронов в единичном объеме? Общее число мест, отданных элек­тронам, равно n а + n i ;, и мы предположим, что когда все элек­троны связаны, то каждому отводится некоторый объем V a . Таким образом, полный атомный объем, занимаемый связан­ными электронами, равен ( n a + n i ) V a , и нашу формулу теперь можно записать в виде

Но формула эта неверна. Мы упустили из вида одно существен­ное обстоятельство: когда один электрон попал в атом, другой электрон уже не может проникнуть в этот же объем! Иначе говоря, не все объемы из числа возможных доступны электрону, который раздумывает, куда бы ему отправиться — в пар или в конденсированное состояние. Здесь возникают не­предвиденные осложнения, в силу которых электрон не может подойти близко к тому месту, где уже находится другой элек­трон — они отталкиваются. По этой причине мы должны считать только ту часть объема, в которой электрон может разместиться. Ведь те объемы, которые уже заняты, нельзя причислять к числу возможных, и только те объемы, которые предоставлены ионам, можно рассматривать как места, вакант­ные для электронов. Тогда, учтя это

обстоятельство, мы найдем, что более точная формула записывается в виде

Эту формулу называют уравнением ионизации, или уравнением Саха. Теперь посмотрим, можем ли мы качественно понять, почему получается формула, подобная этой, если следить за кинетикой процесса.

Прежде всего время от времени, когда электрон сталкива­ется с ионом, они объединяются в атом. Точно так же время от времени атом испытывает столкновение и разваливается на ион и электрон. Скорости обоих процессов должны быть равны. А долго ли электрону и иону искать друг друга? Встречи, конечно, учащаются, если возрастает число электронов в еди­ничном объеме. К этому же приводит и увеличение числа ионов в единичном объеме. Следовательно, полная скорость рекомби­нации пропорциональна произведению числа электронов на число ионов. Далее, полная скорость ионизации в результате столкновений должна линейно зависеть от числа способных к ионизации атомов. Таким образом, скорости обоих процессов сбалансируются тогда, когда установится определенное соот­ношение между произведением n e n i и числом атомов n a . Тот факт, что это соотношение выражается особой формулой, куда входит энергия ионизации W , дает, конечно, несколько большую информацию, но мы можем легко сообразить, что такая формула обязательно должна содержать концентрации электронов, ионов и атомов в комбинации n e n i / n a , которая приводит к постоянной, не зависящей больше от чисел n, а только от тем­пературы, атомных размеров и других постоянных.

Заметим также, что поскольку уравнение содержит числа в единичном объеме и если мы поставим два опыта с одним и тем же полным числом N атомов и ионов, т. е. со строго определен­ным числом ядер, но заключим их в ящики разных объемов, то числа n будут меньше для больших ящиков. Однако отно­шение n en i/n aдолжно оставаться постоянным, поэтому полное число электронов и ионов должно быть больше в большем ящике. Чтобы убедиться в этом, предположим, что в ящик объема V помещено N ядер и их f -я часть ионизована. Тогда n e = fN / V = n i и n a=(1- f ) N / V . В этом случае наше уравнение принимает вид