Feynmann - Feynmann 4

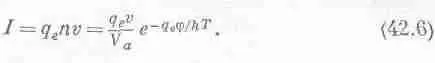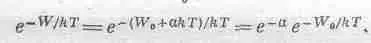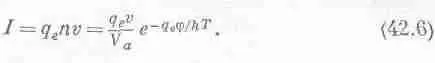
Как определить число электронов, покидающих металл за 1 сек? Очень трудно перечислить все, что может повлиять на выход электрона: легче решить задачу по-другому. Предста­вим, что мы не удаляем вылетевшие электроны, а электроны образуют нечто вроде газа и могут вернуться в металл. В этом случае существует вполне определенная равновесная плотность электронов, которая определяется такой же формулой, как (42.1), где V a , грубо говоря, — объем, отведенный в металле одному электрону, a W = q e j (j —так называемая работа выхода, или разность потенциалов, необходимая для того, чтобы вырвать электрон с поверхности металла). Эта формула подскажет нам, сколько электронов должно находиться в окру­жающем пространстве и проникать в металл, чтобы скомпен­сировать потерю тех электронов, которые покинули металл. Теперь легко подсчитать, сколько электронов уйдет из металла, если мы будем непрерывно откачивать их, потому что число ушедших электронов в точности равно числу электронов, которые должны были бы вернуться в металл, если существовал электронный «пар», плотность которого определяется формулой (42.1). Иначе говоря, электрический ток через единичную площадку равен произведению заряда электрона на число электронов, проходящих за 1 сек через площадку единичной площади; последнее равно произведению числа электронов в единичном объеме на скорость: поэтому, как мы уже много раз видели,

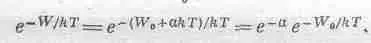
Мы знаем, что 1 эв соответствует kT при температуре, дости­гающей 11 600 град. Нить накаливания радиолампы работает примерно при температуре 1100 град, поэтому экспоненциаль­ный множитель равен примерно е -1 0; когда мы слегка изменяем температуру, экспоненциальный множитель изменяется очень сильно. Это опять основное свойство формул, содержащих ехр(- q e j / kT ). Предэкспоненциальный множитель на самом деле совершенно неверен; оказывается, что поведение электронов в металле правильно описывает квантовая, а не классическая механика, но правильный множитель лишь немного отличается от нашего. Фактически до сих пор никто еще не смог точно вычислить этот множитель, хотя многие при расчетах пользо­вались квантовыми формулами высшего класса. Основная задача состоит в том, чтобы выяснить, не меняется ли W хотя бы мед­ленно с температурой? Если да, то медленно изменяющуюся с температурой величину W нельзя отделить от предэкспоненциальных коэффициентов. Если, например, W зависит от темпера­туры линейно, так что W = W 0 + a kT , то

Такая линейная зависимость W от температуры эквивалентна измененной «постоянной». Попытка точного вычисления пред-экспоненциального множителя очень трудна и обычно бесплодна.

§ 3. Тепловая ионизация

Перейдем теперь к еще одному применению все той же идеи. Теперь речь пойдет об ионизации. Предположим, что газ состоит из великого множества атомов, которые обычно нейтральны, но если газ нагреть, то атомы могут оказаться ионизованными. Нам нужно знать, сколько существует ионов при тех или иных обстоятельствах, т. е. при заданной плотности атомов в единичном объеме и при определенной температуре. Снова придется представить себе ящик, в котором находится N атомов, содержащих в себе электроны. (Если электрон поки­дает атом, то атому присваивается наименование ион, а если атом нейтрален, то говорят просто— атом.) Таким образом, предположим, что в заданный момент в единичном объеме число нейтральных атомов равно n а , число ионов равно n i, а число электронов равно n е . Нужно определить, как связаны эти три числа между собой?

Прежде всего эти числа подчиняются двум условиям или связям. Например, можно как угодно менять различные ус­ловия, температуру и т. д., но сумма n a + n i всегда останется одной и той же, потому что это просто-напросто N — число атомных ядер в ящике. Если в единице объема число ядер сохраняется постоянным, а изменяется, скажем, температура, то, хотя в результате ионизации некоторые атомы превращаются в ионы, общее число атомов и ионов не изменяется. Значит, n e+n i.=N. Другое условие вытекает из того, что если газ в целом электрически нейтрален (и если мы пренебрегаем двой­ной или тройной ионизацией), то число ионов всегда равно числу электронов, или n е=n i. Эти дополнительные условия просто выражают сохранение заряда и сохранение атомов.