Теперь мы могли бы перейти к сферическому зеркалу. Но если вникнуть в смысл сказанного нами ранее, то вполне можно разобрать этот вопрос самостоятельно. Поэтому пусть читатель сам выведет формулы для сферического зеркала, но для этого полезно принять следующие условия:
1) расстояние до объекта s положительно, если точка О расположена слева от поверхности;
2) расстояние до изображения s' положительно, если точка О' расположена справа от поверхности;
3) радиус кривизны поверхности положителен, если центр находится справа от поверхности.
Например, на фиг. 27.2 s, s' и R положительны; на фиг. 27.3 s и R положительны, a s' отрицательна. Для вогнутой поверхности наша формула (27.3) остается справедливой, если считать R отрицательной величиной.
Пользуясь приведенными условиями, можно вывести соответствующую формулу и для зеркала, положив в (27.3) n=-1 (как если бы среда за зеркалом имела показатель преломления -1), и тогда получится правильный результат!
Мы вывели формулу (27.3) простым и элегантным способом, исходя из принципа наименьшего времени; ту же формулу можно, конечно, получить с помощью закона Снелла, если учесть, что углы малы и заменить синусы самими углами.
§ 3. Фокусное расстояние линзы
Рассмотрим теперь другой случай, имеющий большое практическое значение. Большинство линз, которыми мы пользуемся, имеет не одну, а две поверхности раздела. К чему это приводит? Пусть имеется стеклянная линза, ограниченная поверхностями с разной кривизной (фиг. 27.5). Рассмотрим задачу о фокусироваиии пучка света из точки О в точку О'. Как это сделать? Сначала используем формулу (27.3) для первой поверхности, забыв о второй поверхности. Это позволит нам установить, что испускаемый в точке О свет будет казаться сходящимся или расходящимся (в зависимости от знака фокусного расстояния) из некоторой другой точки, скажем О'. Решим теперь вторую часть задачи. Имеется другая поверхность между стеклом и воздухом, и лучи подходят к ней, сходясь к точке О'. Где они сойдутся на самом деле? Снова воспользуемся той же формулой! Находим, что они сойдутся к точке О". Таким образом можно пройти, если необходимо, через 75 поверхностей, последовательно применяя одну и ту же формулу и переходя от одной поверхности к другой!
Имеются еще более сложные формулы, которые могут нам помочь в тех редких случаях нашей жизни, когда нам почему-то нужно проследить путь света через пять поверхностей. Однако если уж это необходимо, то лучше последовательно перебрать пять поверхностей, чем запоминать кучу формул, ведь может случиться, что нам вообще не придется возиться с поверхностями!
Во всяком случае, принцип расчета таков: при переходе через одну поверхность мы находим новое положение, новую точку фокуса и рассматриваем ее как источник для следующей поверхности и т. д.
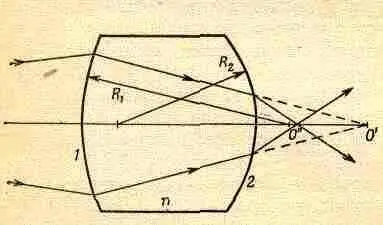
Фиг. 27.5. Построение изображения, даваемого двусторонней линзой.
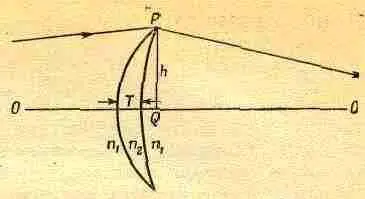
Фиг. 27. 6 . Тонкая линза с двумя положительными радиусами кривизны.
Часто в системах бывает несколько сортов стекла с разными показателями n 1, n 2, ...; поэтому для конкретного решения задачи нам нужно обобщить формулу (27.3) на случай двух разных показателей n 1и n 2. Нетрудно показать, что обобщенное уравнение (27.3) имеет вид
 (27.7)
(27.7)
Особенно прост случай, когда поверхности близки друг к другу и ошибками
из-за конечной толщины можно пренебречь. Рассмотрим линзу, изображенную на фиг. 27.6, и поставим такой вопрос: каким условиям должна удовлетворять линза, чтобы пучок из О фокусировался в О'? Пусть свет проходит точно через край линзы в точке Р. Тогда (пренебрегая временно толщиной линзы Т с показателем преломления n 2) излишек времени на пути ОРО' будет равен (n 1/i 2/2s)+(n 1h 2/2s'). Чтобы уравнять время на пути ОРО' и время на прямолинейном пути, линза должна обладать в центре такой толщиной Т, чтобы она задерживала свет на нужное время. Поэтому толщина линзы Т должна удовлетворять соотношению:
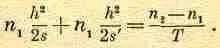 (27.8)
(27.8)
Можно еще выразить Т через радиусы обеих поверхностей R I и R 2. Учитывая условие 3 (приведенное на стр. 27), мы находим для случая R 12(выпуклая линза)
Читать дальше



 (27.7)
(27.7)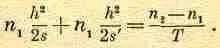 (27.8)
(27.8)










