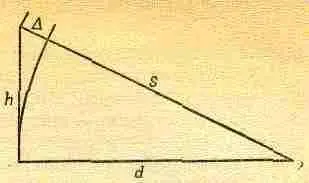
Фиг. 27.1. Треугольник, высота, которого h меньше основания d , a гипотенуза s больше основания.
Оказалось, что наиболее современная и абстрактная теория геометрической оптики, разработанная Гамильтоном, имеет весьма важные приложения в механике, причем в механике она имеет даже большее значение, чем в оптике, поэтому пусть ею занимается курс аналитической механики. А пока, понимая, что геометрическая оптика интересна только сама по себе, мы перейдем к изучению элементарных свойств оптических систем на основе принципов, изложенных в предыдущей главе.
Для дальнейшего нам понадобится одна геометрическая формула: пусть дан треугольник, высота которого h мала, а основание d велико; тогда гипотенуза s (фиг. 27.1) больше основания (нам нужно это знать, чтобы вычислить разность времен на двух различных путях света). Насколько гипотенуза больше основания? Мы можем найти разность D =s-d несколькими способами. Например, s 2-d 2=h 2или (s-d) (s+d)=h 2. Но s-d=D, a s+d~2s. Таким образом,
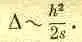 (27.1)
(27.1)
Вот и все, что нам нужно знать из геометрии для изучения изображений, получаемых с помощью кривых поверхностей!
§ 2. Фокусное расстояние для сферической поверхности
Рассмотрим сначала простейший пример преломляющей поверхности, разделяющей две среды с разными показателями преломления (фиг. 27.2). Случай произвольных показателей
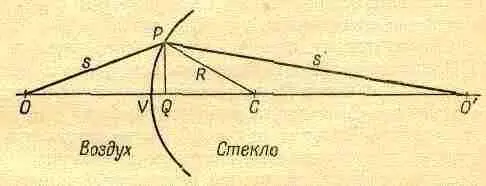
Фиг. 27.2. Фокусировка на преломляющей поверхности.
пусть разберет читатель самостоятельно; нам важно рассказать об идее, задача же достаточно проста и ее можно решить в любом частном случае. Итак, пусть слева скорость света равна 1, а справа 1/n, где n — показатель преломления. Свет в стекле идет медленнее в n раз.
Теперь представим себе точку О на расстоянии s от лицевой поверхности стекла и другую точку О' на расстоянии s' внутри стекла и попытаемся выбрать кривую поверхность так, чтобы каждый луч, вышедший из О и попавший на поверхность в Р, приходил в точку О'. Для этого нужно придать поверхности такую форму, чтобы сумма времени прохождения света на пути от О к Р (т. е. расстояние ОР, деленное на скорость света, равную единице) плюс n-О'Р, т.е. время на пути от Р к О', было постоянной величиной, не зависящей от положения точки Р. Это условие дает уравнение для определения поверхности. В результате получается весьма сложная поверхность четвертого порядка (читатель может вычислить ее для собственного удовольствия с помощью аналитической геометрии). Проще рассмотреть специальный случай s® Ґ, когда кривая получается второго порядка и ее легче определить. Интересно сравнить эту кривую с кривой для фокусирующего зеркала (когда свет приходил из бесконечности), которая, как вы помните, оказалась параболой.
Итак, нужную поверхность сделать нелегко; чтобы сфокусировать свет от одной точке в другую, нужна довольно сложная поверхность. Практически такие сложные поверхности даже не пытаются создать, а пользуются компромиссным решением. Мы не будем собирать все лучи в фокус, а соберем только лучи, достаточно близкие к оси 00'. Раз идеальная форма поверхности столь сложна, возьмем вместо нее сферическую поверхность, которая имеет нужную кривизну у самой оси, и пусть далекие лучи отклоняются от оси, если они того хотят. Сферу изготовить намного проще, чем другие поверхности, поэтому выберем сферу и рассмотрим поведение лучей, падающих на сферическую поверхность. Будем требовать точной фокусировки только для тех лучей, которые проходят вблизи от оси. Иногда эти лучи называют параксиальными, а наша задача — найти условия фокусировки параксиальных лучей. Позже мы обсудим ошибки, связанные с отклонением лучей от оси.
Итак, считая, что Р близко к оси, опустим перпендикуляр PQ длиной h. Если бы наша поверхность была плоскостью, проходящей через Р, то время, затрачиваемое на пути от О к Р, превышало бы время на пути от О к Q, а время на пути от Р к О' превышало бы время от Q к О'. Поверхность стекла должна быть кривой, потому что только в этом случае весь излишек времени компенсируется задержкой при прохождении пути от V к Q! Далее, излишек времени на пути ОР есть h 2/2s, а излишек времени на отрезке О'Р есть nh 2/2s'. Это лишнее время, которое должно компенсироваться временем на пути VQ, накапливается на пути в среде, а не в вакууме. Другими словами, время на пути VQ в n раз больше соответствующего времени в вакууме, а поэтому лишнее время на этом отрезке есть (n-l)VQ. Ну, а какова длина VQ? Если С есть центр сферы с радиусом R, то с помощью уже знакомой нам формулы выводим, что длина VQ есть h 2/2R. В результате мы получаем закон,  (27.2)
(27.2)
Читать дальше


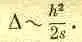 (27.1)
(27.1)
 (27.2)
(27.2)










