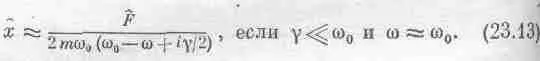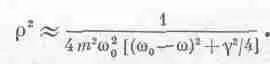Feynmann - Feynmann 2a

Фиг. 23.2. График зависимости r 2 от w .

Очевидно, что если g мало, то основной член в (23.11) — это 1/(w 2 0-w 2) 2, и отклик стремится к бесконечности, если w приближается к w 0. Но эта «бесконеч­ность» — не настоящая бесконечность, потому что даже если w=w 0, то все еще остается слагаемое 1/g 2w 2. Зависимость сдвига фазы от частоты изображена на фиг. 23.3.

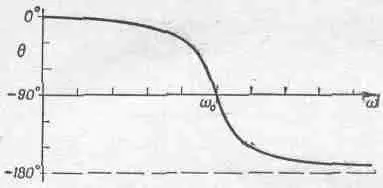
Фиг. 23.3. График зависимости q от w .

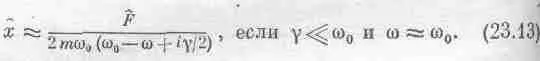
Иногда приходится иметь дело с формулой, немного отли­чающейся от (23.8); она тоже называется «резонансной» и, не­смотря на некоторое отличие от (23.8), описывает те же самые явления. Дело в том, что если значение g очень мало, то наи­более интересная область резонансной кривой лежит около частоты w=w 0, а здесь при малых g формулу (23.8) с большой степенью точности можно заменить приближенной формулой. Поскольку w 2 0-w 2=(w 0-w)(w 0+w), то для w, очень близких к w 0, разность квадратов почти равна 2w 0(w 0-w), a gw можно заменить на gw 0. Значит, w 2 0-w 2+gw»2w 0(w 0-w+ig/2) и

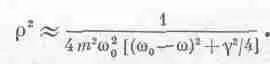
Легко найти и r 2:

А теперь решите сами такую задачу: с увеличением частоты зна­чение r 2сначала растет, достигает при w 0максимума, а потом снова убывает. На каком расстоянии от w 0расположены часто­ты, которым соответствуют значения r 2, вдвое меньшие мак­симального? Покажите, что при очень малом g эти точки от­стоят друг от друга на расстояние Dw=g. Это значит, что ре­зонанс делается более острым по мере того, как влияние тре­ния становится все слабее и слабее.

Другой мерой ширины резонанса может служить «доброт­ность» q=w o/g (чем уже резонанс, тем больше Q ); если Q=1000, то по шкале частот ширина резонансной кривой равна всего 0,001. Резонансной кривой на фиг. 23.2 соответствует Q =5.

Явление резонанса важно потому, что оно проявляется доволь­но часто; описанию некоторых видов этих проявлений мы посвя­тим остаток главы.

§ 3. Электрический резонанс

Простейшие и самые широкие технические применения резо­нанс нашел в электричестве. Имеется довольно много устройств, из которых собираются электрические цепи. Их часто называют пассивными элементами цепи, и бывают они трех типов, хотя в каждый элемент одного типа всегда примешано чуточку эле­ментов других типов. Прежде чем подробно описать эти элементы, заметим, что наше представление о механическом осцилляторе как о массе, подвешенной к концу пружины, всего лишь приближение. В «массе» сосредоточена вовсе не вся масса системы: пружина тоже обладает какой-то массой, пружина тоже инерционна. Точно так же «пружина» не состоит из одной пружины, масса тоже немного упруга, а не абсолютно тверда, как это может показаться. Подпрыгивая вверх и вниз, она слегка изгибается под толчками пружины. Так же обстоит дело и в электричестве. Расположить все предметы по «элемен­там цепи» с чистыми, идеальными характеристиками можно только приближенно. Так как у нас нет времени обсуждать пре­делы таких приближений, мы просто предположим, что они до­пустимы.

Итак, о трех элементах цепи. Первый называется емкостью (фиг. 23.4); в качестве примера емкости могут служить две ме­таллические пластинки, разделенные тонким слоем диэлект­рика.

Фиг. 23.4. Три пассивных элемента цепи.

Если пластинки зарядить, то между ними возникает раз­ность потенциалов. Та же самая разность потенциалов будет между точками А и В, потому что при любой дополнительной разности потенциалов вдоль соединительных проводов заряды стекут по проводам. Таким образом, заданной разности потен­циалов V между пластинками соответствуют определенные заряды + q и - q на каждой пластинке. Между пластинками существует некое электрическое поле; мы даже вывели соответствующую формулу для него (см. гл. 13 и 14)

V=sd/e 0=qd/e 0A , (23.14)

где d — расстояние между пластинками, А — площадь пласти­нок. Заметим, что разность потенциалов линейно зависит от за­ряда. Если построить емкость не из параллельных пластин, а придать отдельным электродам какую-нибудь другую форму, разность потенциалов будет по-прежнему пропорциональна заряду, но постоянную пропорциональности не так-то легко будет рассчитать. Однако надо знать только одно: разность по­тенциалов между концами емкости пропорциональна заряду V = q / C ; множитель пропорциональности равен 1/ С (С и есть емкость объекта).