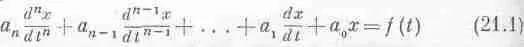Feynmann - Feynmann 2a

Глава 21

ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР

§ 1. Линейные дифференциаль­ные уравнения

§ 2. Гармонический осциллятор

§ 3. Гармоническое движение и движение по окружности

§ 4. Начальные условия

§ 5. Колебания под действием внешней силы

§ 1. Линейные дифференциальные уравнения

Обычно физику как науку делят на не­сколько разделов: механику, электричество и г. п., и мы «проходим» эти разделы один за дру­гим. Сейчас, например, мы «проходим» в основ­ном механику. Но то и дело происходят стран­ные вещи: переходя к новым разделам физики и даже к другим наукам, мы сталкиваемся с уравнениями, почти не отличающимися от уже изученных нами ранее. Таким образом, многие явления имеют аналогию в совсем других об­ластях науки. Простейший пример: распро­странение звуковых волн во многом похоже на распространение световых волн. Если мы достаточно подробно изучим акустику, то обна­ружим потом, что «прошли» довольно большую часть оптики. Таким образом, изучение явле­ний в одной области физики может оказаться полезным при изучении других ее разделов. Хорошо с самого начала предвидеть такое воз­можное «расширение рамок раздела», иначе мо­гут возникнуть недоумения, почему мы тратим столько времени и сил на изучение небольшой задачи механики.

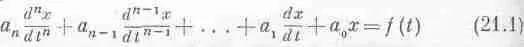
Гармонический осциллятор, к изучению ко­торого мы сейчас переходим, будет встречаться нам почти всюду; хотя мы начнем с чисто меха­нических примеров грузика на пружинке, ма­лых отклонений маятника или каких-то других механических устройств, на самом деле мы бу­дем изучать некое дифференциальное уравне­ние. Это уравнение непрестанно встречается в физике и в других науках и фактически описы­вает столь многие явления, что, право же, стоит того, чтобы изучить его получше. Такое уравне­ние описывает колебания грузика на пружинке, колебания заряда, текущего взад и вперед по электрической цепи, колебания камертона, порождающие звуковые волны, аналогичные колебания электронов в атоме, порождающие световые волны. Добавьте сюда уравнения, описывающие дей­ствия регуляторов, например поддерживающих заданную температуру термостата, сложные взаимодействия в химиче­ских реакциях и (уже совсем неожиданно) уравнения, от­носящиеся к росту колонии бактерий, которых одновременно и кормят и травят ядом, или к размножению лис, питаю­щихся кроликами, которые в свою очередь едят траву, и т. д. Мы привели очень неполный список явлений, которые описы­ваются почти теми же уравнениями, что и механический осцил­лятор. Эти уравнения называются линейными дифференциаль­ными уравнениями с постоянными коэффициентами. Это урав­нения, состоящие из суммы нескольких членов, каждый из которых представляет собой производную зависимой величины по независимой, умноженную на постоянный коэффициент. Таким образом,

называется линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами (все а n — посто­янные).

§ 2. Гармонический осциллятор

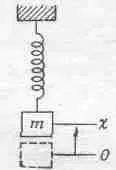
Пожалуй, простейшей механической системой, движение которой описывается линейным дифференциальным уравнением с постоянными коэффициентами, является масса на пружинке. После того как к пружинке подвесят грузик, она немного рас­тянется, чтобы уравновесить силу тяжести. Проследим теперь за вертикальными отклонениями массы от положения равнове­сия (фиг. 21.1).

Фиг. 21.1. Грузик, подвешенный на пружинке.

Простой пример гармонического ос­циллятора.

Отклонения вверх от положения равновесия мы обозначим через х и предположим, что имеем дело с абсо­лютно упругой пружиной. В этом случае противодействующие растяжению силы прямо пропорциональны растяжению. Это означает, что сила равна - kx (знак минус напоминает нам, что сила противодействует смещениям). Таким образом, умно­женное на массу ускорение должно быть равно - kx

m(d 2x/dt 2) =- kx . (21.2)

Для простоты предположим, что вышло так (или мы нужным образом изменили систему единиц), что k / m = 1 . Нам предстоит решить уравнение

d 2x/dt 2=-x. (21.3)

После этого мы вернемся к уравнению (21.2), в котором k и m содержатся явно.