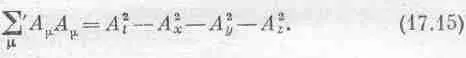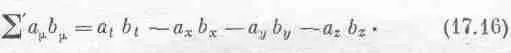Feynmann - Feynmann 2

или в чуть измененных обозначениях:

где i=l, 2, ... относится к сталкивающимся частицам, j=1, 2,... — к частицам, возникающим при столкновении, а m=x, у, z или t . Вы спросите: «А что по осям координат?» Это неважно. Закон верен для любых компонент, при любых осях.

В векторном анализе нам встретилось одно понятие — ска­лярное произведение двух векторов. Что соответствует ему в пространстве-времени? При обычных вращениях неизменной остается величина x 2 + y 2 + z 2 . В четырехмерном мире таким свойством при преобразованиях обладает величина t 2 - х 2 - у 2 - z 2[уравнение (17.3)]. Как можно это записать? Можно было бы, например, пользоваться значком наподобие , но обычно пишут

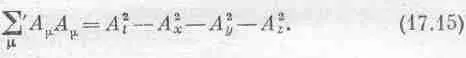
Штрих при S напоминает, что первый, «временной» член по­ложителен, а остальные три отрицательны. Эта величина одна и та же в любой системе координат, и можно назвать ее квадратом длины четырехвектора. Чему равен, например, квадрат длины четырехвектора импульса отдельной частицы?

Ответ: р 2 t - р 2 x- Р 2 у - p 2 z , или, иначе, Е 2-р 2, потому что p t это и есть Е. Чему равно Е 2 - р 2? Должно по условию получиться что-то, что одинаково в любой системе координат, в частности и в системе координат, которая движется вместе с частицей, так что частица в этой системе покоится. Но если частица неподвижна, значит, у нее нет импульса. Значит, у нее остается только энергия, совпадающая в этом случае с ее массой. Итак, Е 2 - р 2=m 2 0, т. е. квадрат длины четырехвектора импульса равен m 2 0.

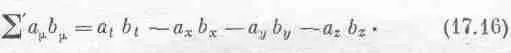
Пользуясь выражением для квадрата вектора, легко изоб­рести скалярное произведение двух четырехвекторов: если один из них а m, а другой b m, то скалярное произведение опре­деляется так:

Это выражение не меняется при преобразовании системы коор­динат.

Следует еще упомянуть о частицах с нулевой массой покоя, например о фотоне — частице света. Фотон похож на частицу тем, что он переносит энергию и импульс. Энергия фотона равна произведению некоторой постоянной (постоянная Планка) на частоту света: E ,= hv . Такой фотон несет с собой и импульс, который (как у всякой частицы) равен постоянной h , деленной на длину волны света: p = h / l . Но у фотона связь между ча­стотой и длиной волны вполне определенна: v — c / l . (Количество волн, проходящих за 1 сек, помноженное на их длину, даст расстояние, проходимое светом в 1 сек, т. е. с.) Мы сходу получаем, что энергия фотона равна его импульсу, умноженному на с, и, далее, полагая с = 1, что энергия равна импульсу. Но это и значит, что масса покоя равна нулю. Давайте вдумаемся в это любопытное обстоятельство. Если фотон — частица с нулевой массой покоя, то что с ним бывает, когда он останав­ливается? Но он никогда не останавливается ! Он всегда движется со скоростью с. Обычная формула для энергии — это m 0 / Ц (1- v 2 ). Можно ли утверждать, что при m 0=0 и v=1 энергия фотона равна нулю? Нет, нельзя; на самом деле фотон может обладать (и обладает) энергией, хоть и не имеет массы покоя, за счет того, что всегда движется со скоростью света!

Мы знаем также, что импульс любой частицы равен про­изведению полной энергии на скорость: p = vE при с=1, или, в обычных единицах, p = vE / c 2 . Для любой частицы, движущейся со скоростью света, р=Е, если с=1. Формулы для энергии фотона в движущейся системе даются по-прежнему уравнением (17.12), но вместо импульса туда нужно подставить энергию, умноженную на с (на 1). Изменение энергии при преобразо­вании означает изменение частоты света. Это явление назы­вается эффектом Допплера; формулу для него легко получить из уравнения (17.12), положив Е=р и E = hv .

Как сказал Минковский: «Пространство само по себе и время само по себе погрузятся в реку забвенья, а останется жить лишь своеобразный их союз».