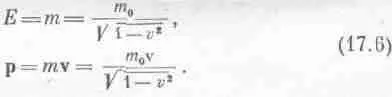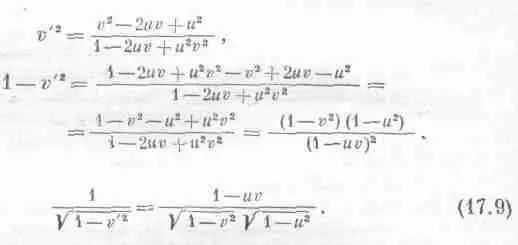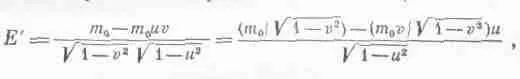Feynmann - Feynmann 2

Напоследок я задам вопрос, ответить на который предо­ставляю вам самим. Если бы внезапно появилась возможность знать, что происходит в области 1 пространства-времени,— возник бы от этого парадокс или нет?

§ 4. Еще о четырехвекторах

Вернемся опять к аналогии между преобразованием Ло­ренца и вращением пространственных осей. Мы уже убедились, что полезно собирать воедино отличные от координат величины, которые преобразуются так же, как и координаты; эти соеди­ненные величины называют векторами, или направленными отрезками. При обычных вращениях немало величин преобра­зуется в точности так же, как х, y , z (например, скорость с тремя компонентами х, у, z ); при переходе из одной системы координат в другую ни одна из компонент не остается прежней, все они приобретают новые значения. Но «сама» скорость, во всяком случае, более реальна, чем любая из ее компонент, и изображаем мы ее направленным отрезком.

Теперь мы спросим: существуют ли величины, которые пре­образуются при переходе от неподвижной системы к движу­щейся так же, как и х, у, z , t ? Наш опыт обращения с векторами подсказывает, что три из этих величин, подобно х, у, z , могли бы представлять собой три компоненты обычного простран­ственного вектора, а четвертая могла бы оказаться похожей на обычный скаляр относительно пространственных вращений: она бы не изменялась, пока мы не перейдем в движущуюся систему координат. Возможно ли, однако, связать с одним из известных «тривекторов» некоторый четвертый объект (ко­торый можно назвать «временной компонентой») таким образом, чтобы вся четверка «вращалась» точно так же, как изменяются пространство и время в пространстве-времени? Мы сейчас покажем, что действительно существует по крайней мере одна такая четверка (на самом деле далеко не одна): три ком­поненты импульса и энергия в качестве временной компоненты преобразуются вместе и образуют так называемый «четырехвектор». Доказывая это, мы избавимся от с тем же приемом, какой употреблялся в уравнении (17.4). Например, энергия и масса отличаются только множителем с 2 и при надлежащем выборе единиц измерения энергия совпадет с массой. Вместо того чтобы писать Е=тс 2 , мы положим Е = т. Если понадо­бится, в окончательных уравнениях можно опять расставить с в нужных степенях.

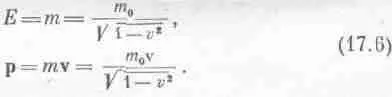
Итак, уравнения для энергии и импульса имеют вид

Значит, при таком выборе единиц получится

Скажем, если энергия выражена в электронвольтах (эв), то чему равна масса в 1 эв? Она равна массе с энергией покоя 1 эв, т. е. m 0c 2=1 эв. У электрона, например, масса покоя равна 0,511·10 6 эв.

Как же будут выглядеть импульс и энергия в новой системе координат? Чтобы узнать это, надо преобразовать уравнения (17.6). Это преобразование легко получить, зная, как пре­образуется скорость. Пусть некоторое тело имело скорость v , а мы наблюдаем за ним из космического корабля, который сам имеет скорость u , и обозначаем соответствующие величины штрихами. Для простоты сперва мы рассмотрим случай, когда скорость v направлена по скорости и. (Более общий случай мы рассмотрим позже.) Чему равна скорость тела v ' по измерениям из космического корабля? Эта скорость равна «раз­ности» между v и u . По прежде полученному нами закону

v’=(v-u)/(1-uv’) (17-8)

Теперь подсчитаем, какой окажется энергия Е' по измерениям космонавта. Он, конечно, воспользуется той же массой покоя, но зато скорость станет v '. Он возведет v ' в квадрат, вычтет из единицы, извлечет квадратный корень и найдет обратную величину

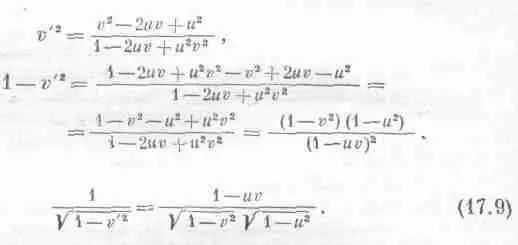
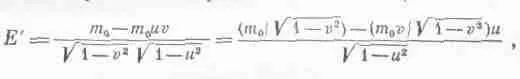
Энергия Е' просто равна массе m 0, умноженной на это выражение. Но нам хочется выразить энергию через нештри­хованные энергию и импульс. Мы замечаем, что

или