Feynmann - Feynmann 2

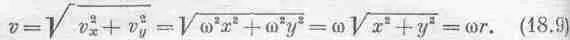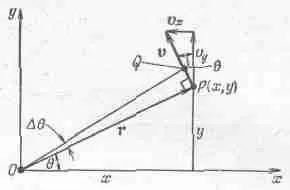
Теперь нам следует связать динамику вращения с дина­микой частиц, из которых сделано тело, т. е. выяснить, как движется каждая данная частица, если угловая скорость со­ставляет столько-то радиан в секунду. Для этого давайте возьмем какую-то частицу, расположенную на расстоянии r от оси, и будем, как обычно, говорить, что в данный момент времени она находится в определенном положении Р(х, у) (фиг. 18.1).

Фиг. 18.1. Кинематика двумер­ного вращения.

Через промежуток времени Dt тело целиком по­вернется на угол Dq, а вместе с ним повернется и наша частица. Хотя расстояние от нее до оси вращения О остается тем же самым, она уже переместится в другую точку, Q . Первое, что хотелось бы знать, это насколько изменятся расстояния х и y. Если обозначить через r длину ОР, то длина PQ будет равна rDq (просто по определению угла). Тогда изменение расстояния х будет равно проекции rDq на ось х

Dz=-PQsinq =-гDqy/r=-y/Dq. (18.6)

Аналогично,

Dy=xDq. (18.7)

Если тело вращается с угловой скоростью w, то, деля обе части равенства (18.6) и (18.7) на Dt, найдем компоненты скорости частицы

v x =-wx и v y =wy. (18.8)

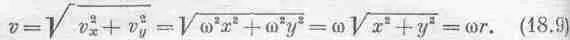
Если же нам требуется абсолютная величина скорости, то мы просто пишем

Не удивительно, что абсолютная величина скорости получи­лась равной wr; это же очевидно; ведь полное пройденное рас­стояние равно rDq, а поэтому расстояние, пройденное за 1 сек, будет rDq/Dt, или rw.

Перейдем теперь к рассмотрению динамики вращения. Здесь следует ввести новое понятие — силу. Давайте посмотрим, нельзя ли изобрести нечто, играющее ту же роль, что и сила в линейном движении. Это нечто мы будем называть моментом силы, или просто моментом. Обычно под силой мы понимаем нечто, заставляющее покоящееся тело двигаться, а то, что заставляет тело вращаться, есть «вращающая», или «крутящая», сила; ее мы называем моментом. Таким образом, качественно момент силы — это кручение; но что такое момент силы коли­чественно? Количественную теорию момента можно получить, изучая работу, затраченную на поворот тела. Этот подход очень хорош и для определения силы: если мы знаем, какая требуется работа, чтобы совершить данное перемещение, то знаем и силу. Чтобы продолжить соответствие между угловыми и линейными величинами, мы должны приравнять работу, которая производится при повороте тела на какой-то угол, к произведению момента на этот угол. Другими словами, при таком определении момента теорема о работе имеет абсолютный аналог: работа есть сила на перемещение, или момент на угол. Это сразу говорит нам, что такое момент количественно. Рас­смотрим, например, твердое тело, вращающееся вокруг оси, на которое действуют различные силы. Сконцентрируем сначала наше внимание на одной силе, приложенной к некоторой точке (х, у). Какую работу мы затрачиваем, поворачивая тело на некоторый малый угол Dq? Нетрудно понять, что она равна

DW=F xDx+F yDy. (18.10)

Теперь нужно только подставить выражения (18.6) и (18.7) для Dx; и Dy и получить

DW=(xF y-yF x) Dq, (18.11)

т. е. работа, которую мы проделали, равна углу, на который было повернуто тело, умноженному на какую-то странную комбинацию сил и расстояний. Эта «странная комбинация» и есть момент. Таким образом, определяя изменение работы как момент, умноженный на угол поворота, мы получаем формулу, выражающую момент через силы. (Это понятно. По­скольку момент не является полностью новым понятием, не зависящим от механики Ньютона, то он должен определенным образом выражаться через силу.)

Пусть теперь на тело действует несколько сил. Тогда ра­бота, производимая этими силами, равна сумме работ от каж­дой силы, так что DW будет иметь вид суммы множества членов: по одному для каждой из сил, однако каждый из них пропор­ционален Dq. Эту величину Dq можно вынести за скобку и получить, что работа равна сумме моментов от всех действу­ющих сил, умноженной на Dq. Эту сумму можно назвать пол­ным моментом сил и обозначить t. Как видите, моменты скла­дываются по обычным законам алгебры, однако, как вы узнаете после, это происходит из-за того, что мы ограничиваемся только плоскими вращениями. Эта ситуация напоминает одномерное движение, в котором силы просто складываются алгебраически; ведь все они в этом случае действуют вдоль одной и той же прямой. В трехмерном пространстве все более сложно. Таким образом, для двумерного вращения