Feynmann - Feynmann 2

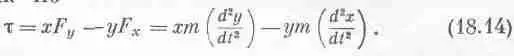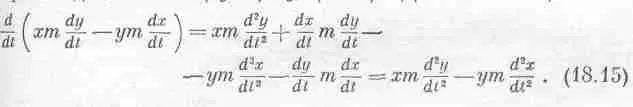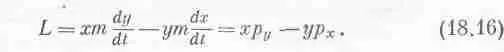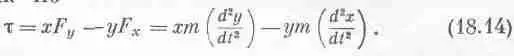
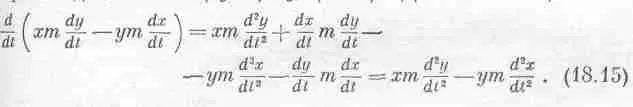
Хотя сразу и не видно, что это выражение является производ­ной от какой-то простой величины, но на самом деле оно равно производной от xm ( dy / dt )- ym ( dx / dt ). Действительно,

Оказывается, таким образом, что момент силы равен скорости изменения со временем некоторой величины! Давайте обратим внимание на эту величину и прежде всего дадим ей имя. Она будет называться моментом количества движения, или угловым моментом, и обозначаться буквой L

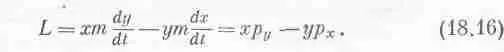
Хотя во всех наших рассмотрениях мы не принимали в рас­чет теорию относительности, тем не менее второе выражение для L верно и при учете ее. Итак, мы нашли, что у обычного импульса также существует вращательный аналог — угловой момент, который связан с компонентами импульса точно так же, как и момент силы связан с компонентами силы! Так что если мы хотим вычислить момент количества движения отно­сительно какой-то оси, то должны взять тангенциальную сос­тавляющую импульса и умножить ее на радиус. Другими сло­вами, угловой момент показывает, насколько быстро движется частица вокруг какого-то центра, ведь он учитывает только тангенциальную часть импульса. Более того, чем дальше от центра удалена линия, по которой направлен импульс, тем больше будет угловой момент. Точно так же, поскольку гео­метрия в этом случае та же, что и в случае момента силы, су­ществует плечо импульса (оно, разумеется, не совпадает с плечом силы, действующей на частицу), которое равно расстоя­нию линии импульса от оси. Таким образом, угловой момент равен просто величине импульса, умноженного на его плечо. Точно так же, как и для момента силы, для углового момента мы можем написать следующие три формулы:

L =хр y - ур х = rp танг =р ·Плечо импульса. (18.17)

Момент количества движения, как и момент силы, зависит от положения оси, относительно которой он вычисляется.

Прежде чем перейти к рассмотрению более чем одной части­цы, применим полученные выше результаты к движению пла­неты вокруг Солнца. В каком направлении действует сила? Конечно, по направлению к Солнцу. А какой при этом будет момент силы? Разумеется, все зависит от того, в каком месте мы выберем ось, однако результат получится совсем простым, если в качестве точки вращения выбрать само Солнце. Посколь­ку момент силы равен силе, умноженной на ее плечо, или ком­поненте силы, перпендикулярной к радиусу r , умноженной на r , то в этом случае нет никакой тангенциальной составляющей силы, а поэтому момент силы относительно оси, проходящей через Солнце, равен нулю. Следовательно, момент количества движения должен оставаться постоянным. Давайте-ка посмот­рим, что это означает. Произведение тангенциальной компонен­ты скорости на массу и радиус, будучи моментом количества движения, должно оставаться постоянным, потому что скорость его изменения есть момент силы, который в нашем случае равен нулю. Это означает, что остается постоянным произведение тангенциальной компоненты скорости на радиус, поскольку масса-то уж, конечно, не изменяется. Но такая величина, ха­рактеризующая движение планеты, уже вычислялась нами раньше. Предположим, что мы взяли маленький промежуток времени Dt. Какое расстояние пройдет планета при своем дви­жении из точки Р в точку Q (фиг. 18.3)? Как велика площадь той области, которую «заметает» прямая, соединяющая пла­нету с Солнцем? Пренебрегая площадью QQ ' P , которая очень мала по сравнению с OPQ , находим, что площадь этой области равна половине основания PQ , умноженного на высоту OR . Другими словами, «заметенная» площадь равна половине про­изведения скорости на ее плечо. Так что скорость изменения этой площади пропорциональна моменту количества движения, который остается постоянным. Итак, мы получим, что закон Кеплера о равных площадях за равные промежутки времени является просто словесным описанием закона сохранения мо­мента количества движения, когда моменты внешних сил от­сутствуют.