Feynmann - Feynmann 1

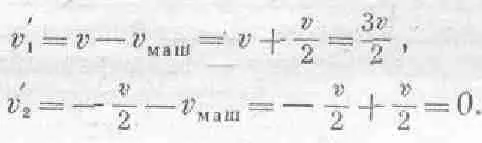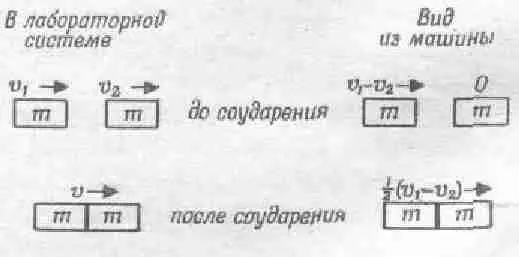
Фиг. 10.5. Другой случай неуп­ругого соударения равных масс.

Обратите внимание, что снова

mv 1+ mv 2=m· 1/ 2(v 1+v 2). (10.6)

Таким образом, принцип относительности Галилея помогает нам разобраться в любом соударении равных масс. До сих пор мы рассматривали движение в одном измерении, однако на основе его становится ясным многое из того, что будет проис­ходить в более сложных случаях соударения: нужно только пустить автомобиль не вдоль направления движения тел, а под каким-то углом. Принцип остается тем же самым, хотя детали несколько усложняются.

Чтобы экспериментально проверить, действительно ли тело, летящее со скоростью v после столкновения с покоящимся телом той же массы, образует новое тело, летящее со скоростью v /2, проделаем на нашей замечательной установке следующий опыт. Поместим в желоб три тела с одинаковыми массами, два из которых соединены цилиндром со взрывателем, а третье на­ходится вблизи одного из них, хотя и несколько отделено от него. Оно снабжено клейким амортизатором, так что прилипает к тому телу, которое ударяет его. В первое мгновение после взрыва мы имеем два объекта с массами m , движущимися со скоростью v каждое. В последующее мгновение одно из тел сталкивается с третьим и образует новое тело с массой 2т, которое, как мы полагаем, должно двигаться со скоростью v /2. Но как проверить, что скорость его действительно v/2? Для этого мы вначале установим тела таким образом, чтобы расстояния до концов желоба относились как 2:1, так что первое тело, которое продолжает двигаться со скоростью v, должно пролететь за тот же промежуток времени вдвое большее расстояние, чем скрепившиеся два других тела (с учетом, ко­нечно, того малого расстояния А, которое второе тело прошло до столкновения с третьим). Если мы правы, то массы m и 2m должны достичь концов желоба одновременно; так оно и про­исходит на самом деле (фиг. 10.6).

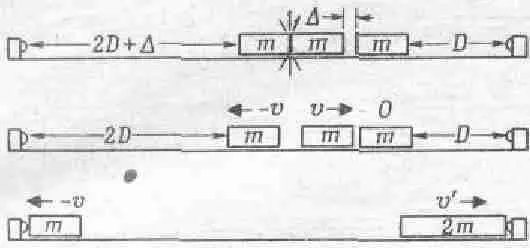
Фиг. 10.6. Экспериментальная проверка того факта, что масса т, ударяя со скоростью v массу m , образует тело с массой 2 m и скоростью v /2.

Следующая проблема, которую мы должны решить: что получится, если тела имеют разные массы. Давайте возьмем массы m и 2m и устроим между ними взрыв. Что произойдет тогда? С какой скоростью полетит масса 2т, если масса m летит со скоростью v? Фактически нам нужно повторить только что проделанный эксперимент, но с нулевым зазором между вторым и третьим телом. Разумеется, что при этом мы получим тот же результат — скорости тел с массами m и 2m должны быть соответственно равны - v и v /2. Итак, при разлете тел с массами m и 2m получается тот же результат, что и при симметричном разлете двух тел с массами m с последующим неупругим соударением одного из этих тел с третьим, масса которого тоже равна m. Более того, отразившись от концов, каждое из этих тел будет лететь с почти той же скоростью, но, конечно, в об­ратном направлении, и после неупругого соударения они оста­навливаются.

Перейдем теперь к следующему вопросу. Что произойдет, если тело с массой m и скоростью v столкнется с покоящимся телом с массой 2m? Воспользовавшись принципом относитель­ности Галилея, можно легко ответить на этот вопрос. Попросту говоря, нам нужно опять садиться в машину, идущую со скоростью - v /2 (фиг. 10.7), и наблюдать за только что описанным процессом.

Фиг. 10.7. Неупругое соударение между телами с массами m и 2 m .

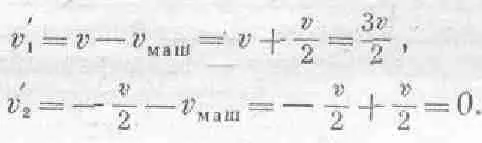
Скорости, которые мы при этом увидим, будут равны

После соударения масса 3m покажется нам движущейся со скоростью v /2. Таким образом, мы получили, что отношение скоростей до и после соударения равно 3:1, т. е. образовав­шееся тело с массой 3m будет двигаться в три раза медленней; И в этом случае снова выполняется общее правило: сумма произведений массы на скорость остается той же как до, так и после соударения: то + 0 равно 3 m · v /3. Вы видите, как по­степенно шаг за шагом устанавливается закон сохранения им­пульса.