Feynmann - Feynmann 1

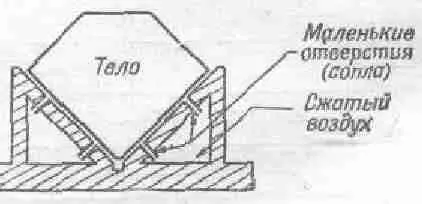
Фиг. 10.1. Воздушный желоб (вид с торца).

В этом устройстве нет никаких трущихся деталей — вопрос, который очень беспокоил Галилея. Он не мог поставить эксперимента со скользящими телами, ибо они не скользили свободно, но о помощью чудесного желоба мы можем теперь избавиться от трения. Наши тела будут лететь без помех, а скорость их, со­гласно предвидению Галилея, будет оставаться постоянной. Это достигается тем, что тело поддерживается воздушной по­душкой, а поскольку трение о воздух очень мало, то тело пла­нирует практически с постоянной скоростью, если на него не действуют никакие силы. Возьмем сначала два скользящих бруска, вес или массы которых с большой точностью равны друг другу (практически измеряется вес, но он, как вы знаете, пропорционален массе), и поместим между ними небольшой взрыватель в закрытом цилиндре (фиг. 10.2).

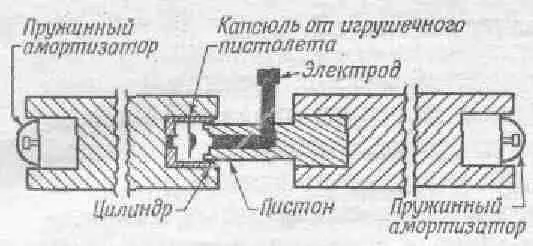
Фиг. 10.2. Продольный разрез скользящего бруска, скрепленного со взрывным цилиндром.

Всю эту систему устанавливаем в центре желоба и электрической искрой под­жигаем взрыватель. Что же произойдет? Если массы брусков одинаковы, то они, разлетевшись в стороны, одновременно до­стигнут концов желоба. Там они отскакивают от ограничите­лей, сталкиваются и слипаются в центре, точно в том же месте, откуда разлетелись (фиг. 10.3).

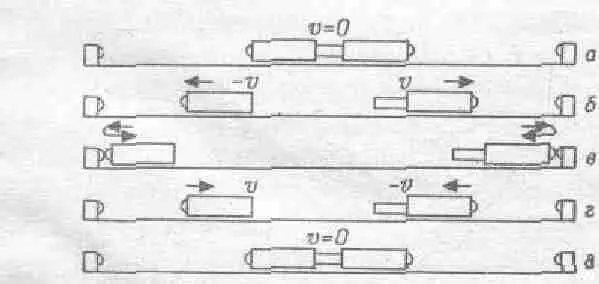
Фиг. 10.3. Схема эксперимента с равными массами.

Это интересный опыт. И в дей­ствительности происходит все так, как мы рассказали.

Теперь на очереди проблема посложнее. Допустим, мы имеем две массы, причем одна движется со скоростью v , а другая стоит на месте. Затем первая ударяет по второй и они слипаются. Что произойдет дальше? Образуется одно тело с массой 2m , которое как-то будет двигаться. Но с какой скоростью? Вот в чем вопрос. Чтобы ответить на него, предположим, что мы едем вдоль желоба на автомобиле. Все законы физики должны при этом выглядеть точно так же, как и прежде, когда мы стояли на месте. Мы начали с того, что если столкнуть два тела с рав­ными массами и одинаковыми скоростями v , то после слипания они останавливаются. А теперь представьте, что в это время мы катим на автомобиле со скоростью — v . Какую же картину Мы увидим? Ясно, что одно из тел, поскольку оно все время летит рядом с автомобилем, будет казаться нам неподвижным. Второе же, которое движется навстречу со скоростью v , покажется нам несущимся с удвоенной скоростью 2 v (фиг. 10.4).

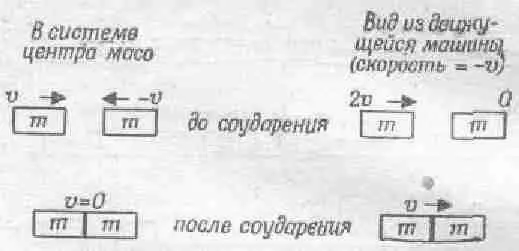
Фиг. 10.4, Неупругое соударение равных масс.

Наконец, образовавшееся после соударения и слипания тело будет ка­заться нам летящим со скоростью v . Отсюда мы делаем вывод, что если тело, летящее со скоростью 2 v , ударяется о покоящееся тело той же массы и прилипает к нему, то образовавшееся тело будет двигаться со скоростью v , или (что математически то же самое) тело со скоростью v , ударяясь о покоящееся тело той же массы и прилипая к нему, образует тело, движущееся со скоростью v /2. Заметьте, что если умножить массы тел на их скорости и сложить их, то получим одинаковый результат как до столкновения ( mv + 0), так и после (2 m · v /2). Вот как обстоит дело, если тело, обладающее скоростью v , столкнется с телом, находящимся в покое.

Точно таким же образом можно определить, что произойдет, когда сталкиваются два одинаковых тела, каждое из которых движется с произвольной скоростью.

Пусть одно тело летит со скоростью v 1 , а другое — со ско­ростью v 2в том же направлении (v 1>v 2 ). Какова будет их ско­рость после соударения? Давайте снова сядем в машину и по­едем, скажем, со скоростью v 2 . Тогда одно из тел будет казаться нам стоящим на месте, а второе — налетающим на него со ско­ростью v 1- v 2 . Эта ситуация уже знакома нам, и мы знаем, что после соударения скорость нового тела по отношению к машине будет равна 1/ 2 ( v 1 - v 2 ). Что же касается действитель­ной скорости относительно земли, то ее можно найти, прибавив скорость автомобиля: v = 1/ 2(v 1-v 2) +v 2или 1/ 2(v 1+v 2) (фиг. 10.5).