Марк Хэддон - Загадковий нічний інцидент із собакою

Я ходив із Матір’ю в книгарню й купив книжку під назвою «Іспит рівня “А” з вищої математики», а Батько сказав місіс Ґасконь, що наступного року я складатиму іспит рівня «А» з вищої математики, і вона погодилася.

Я його складу й отримаю оцінку «А». А за два роки я складу іспит рівня «А» з фізики й отримаю оцінку «А».

А тоді, коли я це зроблю, то вступлю до університету в іншому місті. І це не обов’язково має бути Лондон, оскільки мені не подобається Лондон, і університети є в багатьох інших містах, і не всі вони великі. Я житиму в квартирі з садом і окремим туалетом. І я візьму з собою Піщаника, книжки й комп’ютер.

Потім я отримаю диплом із відзнакою й стану вченим.

І я знаю, що здатен на це, оскільки я сам їздив до Лондона й оскільки я розгадав таємницю «Хто вбив Веллінгтона?», знайшов свою маму, був хоробрим і написав книжку, а це означає, що я здатен на все.

Задача

Доведіть, що:

«Трикутник зі сторонами, які можна виразити формулами n 2+ 1, n 2– 1 та 2n (де n > 1), є прямокутним».

Доведіть від супротивного, що обернене твердження невірне.

Розв’язання

Спочатку нам треба визначити, яка зі сторін трикутника, сторони якого виражені формулами n 2+ 1, n 2– 1 та 2n (де n > 1), є найдовшою. Це можна виразити так:

n 2+ 1 – 2n = (n – 1) 2,

і якщо n > 1, тоді (n – 1) 2> 0.

Отже, n 2+ 1 – 2n > 0,

отже, n 2+ 1 > 2n.

Аналогічно (n 2+ 1) – (n 2– 1) = 2,

отже, n 2+ 1 > n 2– 1.

Це означає, що n2 + 1 є найдовшою стороною трикутника, сторони якого виражені формулами n 2+ 1, n 2– 1 та 2n (де n > 1).

Це також можна продемонструвати за допомогою наступного графіка (але це нічого не доводить):

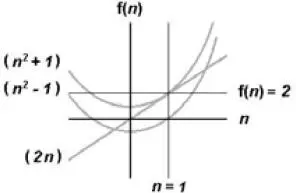
Згідно з теоремою Піфагора, якщо сума квадратів двох катетів дорівнює квадрату гіпотенузи, то цей трикутник є прямокутним. Отже, для того, щоби довести, що цей трикутник прямокутний, нам треба показати це на наступному прикладі.

Сума квадратів двох катетів дорівнює (n 2– 1) 2+ (2n) 2

(n 2– 1) 2+ (2n) 2=

= n 4– 2n 2+ 1 + 4n 2= n 4+ 2n 2+ 1.

Квадрат гіпотенузи дорівнює (n2 + 1)2

(n 2+ 1) 2= n 4+ 2n 2+ 1.

Отже, сума квадратів катетів дорівнює квадрату гіпотенузи, і цей трикутник є прямокутним.

А обернене твердження від «Трикутник зі сторонами, які можна виразити формулами n 2+ 1, n 2– 1 та 2n (де n > 1), є прямокутним» — це «Прямокутний трикутник має сторони, довжину яких можна виразити формулами n 2+ 1, n 2– 1 та 2n (де n > 1)».

А доведення від супротивного означає, що треба довести існування прямокутного трикутника, сторони якого не можна виразити формулами n 2+ 1, n 2– 1 та 2n (де n > 1).

Позначимо гіпотенузу прямокутного трикутника ABC як AB.

Нехай AB = 65,

нехай BC = 60.

Отже CA = √ (AB2 – BC2) =

= √ (652 – 602) = √ (4225 – 3600) = √ 625 = 25.

Нехай AB = n 2+ 1 = 65,

тоді n = √ (65 – 1) = √ 64 = 8,

отже, √ (n 2– 1) = 64 – 1 = 63 ≠ BC = 60 ≠ CA = 25

і 2n = 16 ≠ BC = 60 ≠ CA = 25.

Таким чином, трикутник ABC є прямокутним, але в нього немає сторін, які можна виразити формулами n 2+ 1, n 2– 1 та 2n (де n > 1). ЩТД (Що й треба було довести).

Я знайшов цю книжку в міській бібліотеці, коли одного разу Мати повезла мене до міста.

Це не метафора, а порівняння, тобто він дійсно мав такий вигляд, наче в його ніздрях ховалися дві маленькі миші, і якщо ви спробуєте уявити голову чоловіка, у якого з ніздрів стирчать дві малесенькі миші, то зрозумієте, який вигляд мав поліцейський інспектор. Порівняння — це не брехня, тільки якщо це доречне порівняння.

Але я б не став запивати шоколадні подушечки чаєм, оскільки і подушечки, і чай коричневі.

Якось я ні з ким не розмовляв упродовж 5 тижнів.

Коли мені було 6 років, то Мати змушувала мене пити полуничні коктейлі для схуднення з мірчої склянки, і ми влаштовували змагання з того, як швидко я зможу випити чверть літра.

Люди кажуть, що треба завжди говорити правду. Але вони не дотримуються цього правила, оскільки не можна казати старим людям, що вони старі, і не можна казати людям, що від них погано пахне або що дорослий пукнув. І не можна казати: «Ти мені не подобаєшся», якщо тільки та людина не заподіяла тобі лиха.

Дурниці — це такі речі, як, наприклад, вивалити на кухонний стіл банку арахісового масла та розрівняти його ножем так, щоби воно рівномірно покривало стіл до самих країв, або палити речі на газовій плиті, щоб подивитися, що з ними станеться, як-то: черевики, фольгу чи цукор.