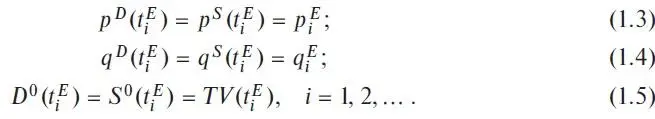Анатолий Кондратенко - Вероятностная теория фондовых бирж

Отмеченная аналогия с физической системой наводит на мысль использовать аналогичный математический аппарат, аналитический и графический. На рис. 1.3, для начала, мы даем графическое представление этих траекторий движения агентов в зависимости от времени с помощью подходящих систем координат время – цена ( T, P ) и время – количество ( T, Q ), аналогично тому, как происходит построение траекторий частиц в классической механике. Заметим, что рис. 1.3 отражает определенную стандартную ситуацию на рынке, когда покупатель и продавец намеренно встречаются в момент времени t 1 и начинают обсуждать потенциальную сделку путем взаимного обмена информацией об их условиях, прежде всего желаемых цен и количества товара. Во время переговоров они непрерывно изменяют свои котировки до тех пор, пока не соглашаются на окончательные условия по цене p 1 E и количеству q 1 E в момент времени t 1 E . Такая простейшая «переговорная» рыночная модель применима, например, для экономики вымышленного острова, на котором, скажем для определенности, раз в году путем переговоров происходит торговля зерном между фермером и охотником. Для определенности, будем считать, что они используют для расчетов американский доллар, $. Для наглядности, на рис. 1.3, как и на последующих рисунках, мы используем стрелки для отражения направления движения агентов во время рыночного процесса.

Итак, в нашей переговорной классической модели вплоть до момента t 1 рынок находится в простейшем состоянии покоя, здесь нет торговли вообще. В момент времени t 1 на рынке появляются покупатель и продавец зерна, которые устанавливают свои начальные желаемые цены и количество зерна: p D ( t 1 ), p S ( t 1 ) и q D ( t 1 ), q S ( t 1 ). Точки P и V на графике показывают положение покупателя и продавца в начальный момент времени t 1 , когда начинаются торговые переговоры. Естественно, желания покупателя и продавца сразу не совпадают, покупатель хочет низкую цену, но продавец борется за более высокую цену. Однако оба нуждаются в достижении понимания и последующего заключения сделки, в противном случае фермер и охотник будут иметь трудный следующий год. Переговорный процесс продолжается, рыночный процесс изменения агентами их котировок отражает его ход. Как результат, позиции рыночных агентов сходятся, и они совпадают в момент времени t 1 E , который соответствует точке пересечения траекторий E 1на графиках.

На взаимовыгодных условиях в момент времени t 1 E осуществляется добровольная сделка. Далее рынок снова погружается в состояние покоя до следующего урожая и выставления его на продажу в следующем году в момент времени t 2 .

Предположим, для определенности, что урожай в новом сезоне вырос, поэтому q S ( t 2 ) > q S ( t 1 ). В этом случае продавец, очевидно, вынужден сразу установить стартовую цену ниже,

p S ( t 2 ) < p S ( t 1), пока покупатель, воспользовавшись возможностью, также понижает цену и увеличивает свое количество зерна: p D ( t 2 ) < p D ( t 1 ) и q D ( t 2 ) > q D ( t 1 ). В этом случае естественно ожидать, что траектории покупателя и продавца будут немного различаться, и соглашение между покупателем и продавцом будет достигаться с другими параметрами, чем в предыдущий раунд торгов.

Условно мы будем описывать ситуацию на рынке в каждый момент времени с помощью множества реальных рыночных цен и количеств реальных сделок, которые действительно происходят на рынке. Как видно из рис. 1.3, в нашей модели реальные сделки происходят на рынке только в такие моменты времени, например, t 1 E и t 2 E когда справедливы следующие условия рыночного равновесия (точки E 1 на рис. 1.3):

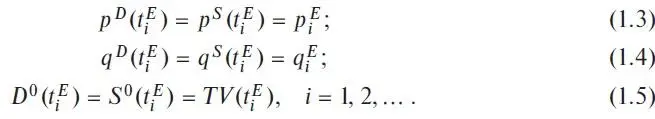
1.6.3. КОНЦЕПЦИЯ СПРОСА И ПРЕДЛОЖЕНИЯ В КЛАССИКЕ

В формулах (1.3)-(1.5) мы использовали несколько новых понятий и определений, смысл которых требует разъяснения. Мы представим его довольно подробно, поскольку это важно для понимания последующего изложения теории. Во-первых, в современной экономической теории концепция S&D играет одну из центральных ролей. То же самое относится и к вероятностной экономической теории, которую, как мы говорили выше, в определенной мере можно трактовать как теорию спроса и предложения. Интуитивно, на качественном описательном уровне все экономисты понимают, что означает эта концепция. Сложности и расхождения появляются только на практике при попытках дать математическое толкование этим понятиям и развить адекватный метод их вычисления и измерения. Для этой цели были развиты различные теории, содержащие разные математические модели S&D. В этих теориях различные функции S&D используются для формального определения и количественного описания S&D.