Нихиль Будума - Основы глубокого обучения

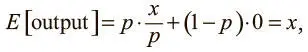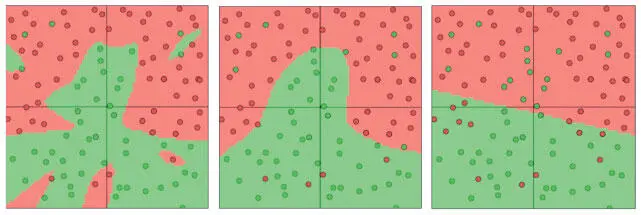
Рис. 2.15. Визуализация нейросетей, обученных с показателями регуляризации 0,01, 0,1 и 1 (в таком порядке)

Еще один распространенный вариант — L1-регуляризация . Здесь мы добавляем значение λ|w| для каждого веса w в нейросети. L1-регуляризация обладает интригующим свойством: в ходе оптимизации векторы весов становятся очень разреженными (очень близкими к 0). Иными словами, нейроны начинают использовать небольшое количество самых важных входов и становятся устойчивыми к шуму на входе. А векторы весов, полученные при L2-регуляризации, обычно равномерны и невелики. L1-регуляризация очень полезна, когда вы хотите понять, какие именно свойства вносят вклад в принятие решения. Если такой уровень анализа свойств не нужен, мы используем L2-регуляризацию: она на практике работает лучше.

Максимальные ограничения нормы имеют схожую цель: это попытка предотвратить слишком большие значения θ, но более непосредственная [15]. Максимальные ограничения нормы задают абсолютную верхнюю границу для входного вектора весов каждого нейрона и при помощи метода проекции градиента устанавливают ограничение. Иными словами, каждый раз, когда шаг градиентного спуска изменяет входящий вектор весов, так что || w || 2 > c, мы проецируем вектор обратно на шар (центр которого расположен в исходной точке) с радиусом c . Типичные значения c — 3 и 4. Примечательно, что вектор параметров не может выйти из-под контроля (даже если нормы обучения слишком высоки), поскольку обновления весов всегда ограничены.

Совсем иной метод борьбы с переобучением — прореживание (Dropout) , который особенно популярен у специалистов по глубоким нейросетям [16]. При обучении он используется так: нейрон становится активным только с некой вероятностью p (гиперпараметр), иначе его значение приравнивается к 0. На интуитивном уровне можно решить, что это заставляет нейросеть оставаться точной даже в условиях недостатка информации. Сеть перестает быть слишком зависимой от отдельного нейрона или их небольшого сочетания. С точки зрения математики прореживание препятствует переобучению, давая возможность приблизительно сочетать экспоненциально большое количество архитектур нейросетей, причем эффективно. Процесс прореживания показан на рис. 2.16.

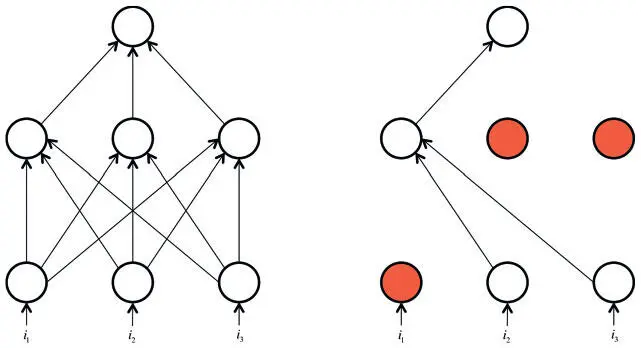
Рис. 2.16. Прореживание помечает каждый нейрон сети как неактивный с некой случайной вероятностью на каждом этапе обучения

Прореживание — понятный процесс, но стоит учесть несколько важных моментов. Во-первых, нужно, чтобы выходные значения нейронов во время тестирования были эквивалентны ожидаемым выходным значениям в процессе обучения. Мы можем добиться этого наивным способом, масштабировав параметры в тесте. Например, если p = 0,5, нейроны должны вдвое уменьшить выходные значения в тесте, чтобы обеспечить те же (ожидаемые) параметры в ходе обучения. Ведь выходное значение нейрона равно 0 с вероятностью (1 − p). И если до прореживания оно равнялось x , после прореживания ожидаемое значение будет E [output] = px + (1 − p) 0 = px . Но такое применение операции нежелательно, поскольку предполагает масштабирование выходных значений нейрона во время тестирования. Результаты тестов очень важны для оценки модели, и предпочтительнее использовать обратное прореживание , при котором масштабирование происходит в процессе обучения, а не тестирования. Выходное значение любого нейрона, активность которого не заглушена, делится на p перед передачей его на следующий уровень. Теперь

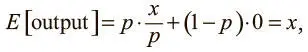
что позволит не прибегать к произвольному масштабированию выходных значений нейрона во время тестирования.

Мы познакомились с основами обучения нейронных сетей с прямым распространением сигнала, поговорили о градиентном спуске, алгоритме обратного распространения ошибки, а также методах борьбы с переобучением. В следующей главе мы применим полученные знания на практике, используя библиотеку TensorFlow для эффективного создания первых нейросетей. В главе 4 мы вернемся к проблеме оптимизации целевых функций для обучения нейросетей и разработки алгоритмов, значительно повышающих качество обучения. Эти улучшения позволят обрабатывать гораздо больше данных, а следовательно, и строить более сложные модели.