Дуглас Хаббард - Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе]

Однако у Guinness уже были проблемы с разглашением коммерческой тайны, и служащим компании было запрещено публиковать любую информацию о бизнес-процессах. Госсет понимал значение своей работы, но ему сильнее хотелось рассказать о своей идее, чем добиться немедленного признания. Поэтому он опубликовал статью под псевдонимом «Стьюдент». И хотя истинный автор давно известен, практически во всех работах по статистике метод называется t-статистикой Стьюдента.

Вид распределения Стьюдента напоминает обсуждавшееся нами ранее нормальное распределение. Но в случае очень малых выборок его форма становится намного уплощеннее и шире. Рассчитанный с помощью t-статистики 90-процентный CI намного шире (то есть неопределеннее), чем в случае нормального распределения. Если размер выборки больше 30, то график t-распределения практически совпадает с нормальным распределением.

И для одного, и для другого типа распределения существует сравнительно простой (по сравнению со многими другими статистическими методами) способ расчета 90-процентного доверительного интервала для среднего значения генеральной совокупности. Кому-то наши расчеты могут показаться слишком сложными, а те, кто уже знаком с данным методом, скажут, что мы просто пересказываем содержание учебников по статистике. Пусть первые подождут, пока мы не рассмотрим в следующей главе намного более простое решение, а вторые просто пропустят этот материал. Адресуя свои пояснения читателям, которые отнесут себя к средней категории, я старался сделать их как можно более простыми для восприятия. Вот как мы могли рассчитать 90-процентный CI в предыдущем примере, отобрав всего пять леденцов.

1. Рассчитаем сначала дисперсию выборки (этим понятием мы позднее будем часто пользоваться):

а) рассчитаем средний вес отобранных леденцов: (1,4 + 1,4 + 1,5 + 1,6 + 1,1)/5 = 1,4;

б) вычтем это среднее из каждого значения в выборке и возведем полученные результаты в квадрат: (1,4–1,4) 2= 0; (1,5–1,4) 2= 0,01 2и т. д.;

в) суммируем все квадраты и разделим на размер выборки минус единица: (0 + 0 + 0,01 + 0,04 + 0,09)/(5–1) = 0,035.

2. Разделим дисперсию выборки на ее размер и извлечем из полученного результата квадратный корень. В электронной таблице мы записали бы «=SQRT (0,035/5)» и получили 0,0837.

(В работах по статистике это называется средним квадратичным отклонением.)

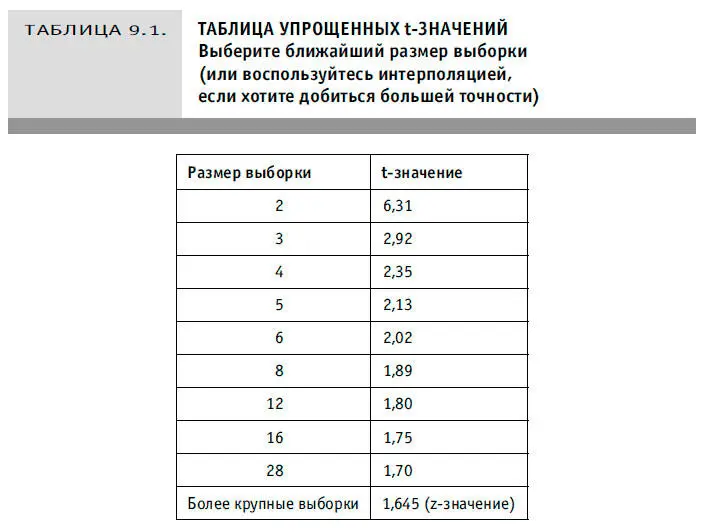
3. Найдем в таблице 9.1 (таблице упрощенных значений t-статистики) значение t, соответствующее размеру выборки: для выборки, состоящей из пяти объектов, t = 2,13. Обратите внимание, что для очень больших выборок t близко к z-значению (нормальное распределение) 1,645.

4. Умножим найденное t-значение на результат этапа 2: 2,13 × 0,0837 = 0,178. Это ошибка выборки в граммах.

5. Суммируем ошибку выборки и средний вес леденца, чтобы получить верхнюю границу 90-процентного CI, а затем вычтем ее из среднего веса, чтобы получить нижнюю границу: верхняя граница = 1,4 + 0,178 = 1,578; нижняя граница = 1,4–0,178 = 1,222.

Итак, выбрав всего пять леденцов, мы получили 90-процентный CI, составляющий 1,222–1,578. Аналогично рассчитывают доверительный интервал и для более крупных выборок. Единственная разница заключается в том, что z-значение, необходимое для этого, всегда будет составлять 1,645 (с ростом размера выборки оно не увеличится).

На рисунке 9.1 представлен общий результат решения другой гипотетической задачи с использованием t-статистики. Это могло быть определение средней партии пива, сваренного в компании Guinness, среднего времени, проводимого покупателями в очередях, или среднего размера обуви жителей штата Небраска. В любом случае необходимо определить 90-процентный CI для среднего значения генеральной совокупности, хотя по каким-то причинам (экономические факторы, ограниченность во времени или несогласие жителей штата Небраска на измерение размеров их ног) размер выборки из подобных совокупностей составлял бы не десятки и сотни, а всего несколько образцов.

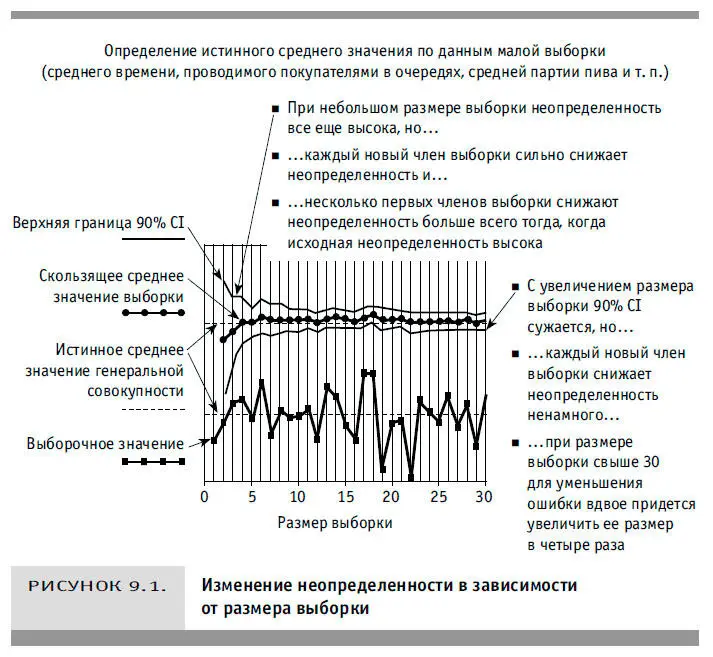
На этом рисунке нижняя ломаная линия — график значений выборки, пунктир — истинное среднее значение генеральной совокупности. Одни значения выборки выше этого среднего, другие ниже. Фактических значений на рисунке нет, но для наших целей смысл понятен. В верхней части рисунка вы видите три кривые, левые края которых образуют своеобразную «воронку торнадо». Средняя линия — график скользящей средней выборки (сначала среднее из первых трех значений, затем среднее из первых четырех значений и т. д.), которая сравнивается с истинным средним генеральной совокупности, представленным прямой пунктирной линией. Две внешние кривые — графики верхней и нижней границ 90-процентного доверительного интервала, пересчитываемого после каждого нового пополнения выборки.