Anil K. Chopra - Earthquake Engineering for Concrete Dams

The traditional design loadings for gravity dams include seismic water pressures in addition to the hydrostatic pressures, as specified by various formulas (U.S. Army Corps of Engineers 1958; Bureau of Reclamation 1966). These formulas differ somewhat in detail and in numerical values but not in underlying assumptions; they are all based on the classical results (Westergaard 1933; Zangar 1952) derived from analyses that assumed the dam to be rigid and water to be incompressible. One of these formulas specifies the seismic water pressure p e= cswH , where c is a coefficient that varies from zero at the water surface to about 0.7 at the reservoir bottom, s is the seismic coefficient, w is the unit weight of water, and H is the total depth of water. For a seismic coefficient of 0.1, the additional water pressure at the base of the dam is about 7% of the hydrostatic pressure; and pressure values at higher elevations are even smaller. As a result, these additional water pressures have little influence on the computed stresses and hence on the geometry of the gravity section that satisfies the traditional design criteria.

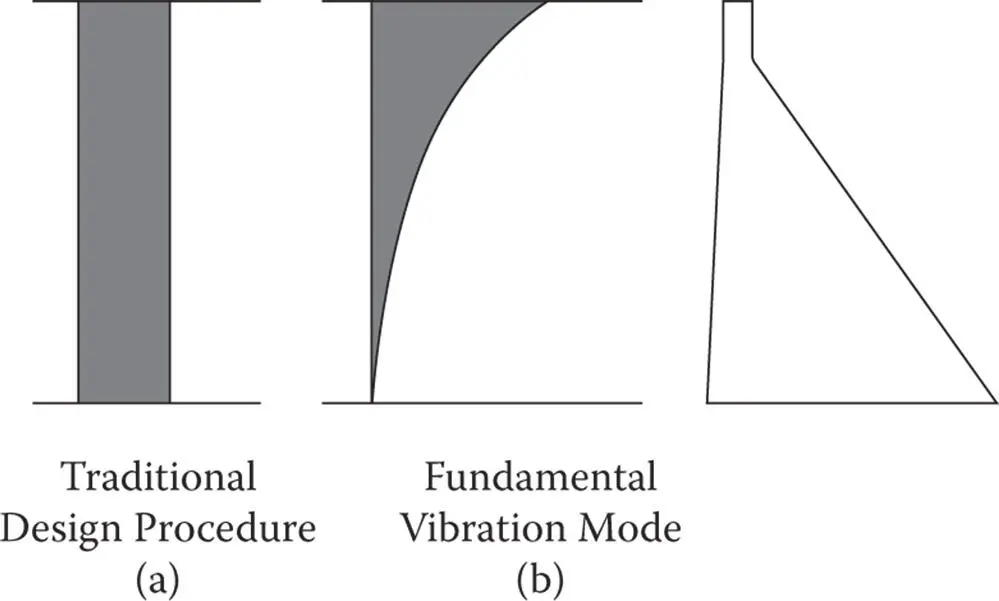
Figure 1.3.3Distribution of seismic coefficients over dam height in traditional design and for the fundamental vibration mode.

Source: Adapted from Chopra (1978).

On the other hand, earthquake‐induced stresses in gravity dams are much larger when dam–water interaction arising from deformations of the dam and water compressibility effects are considered, as will be demonstrated in Chapters 2and 6. It is apparent, therefore, that hydrodynamic effects are considerably underestimated because of assumptions implicit in traditional design forces.

As mentioned earlier, traditional analysis and design procedures ignore interaction between the dam and foundation. However, such interaction has very significant influence on the dynamics of the system, and, hence, on the earthquake‐induced stresses. This will be demonstrated in Chapters 3and 6.

Finally, the static overturning and sliding criteria that have been used in traditional design procedures for gravity dams have little meaning in the context of oscillatory response to earthquake motions.

Traditionally, the dynamic response of the system has not been considered in defining the earthquake forces in the design of arch dams. For example, the U.S. Bureau of Reclamation (1965) stated: “The occurrence of vibratory response of the earthquake, dam, and water is not considered, since it is believed to be a remote possibility.” Thus, the forces associated with the inertia of the dam were expressed as the product of a seismic coefficient – which was constant over the surface of the dam with a typical value of 0.10 or less – and the weight of the dam. Water pressures, in addition to the hydrostatic pressure, were specified in terms of the seismic coefficient and a pressure coefficient that was the same as for gravity dams, defined in Section 1.3.3. This pressure coefficient was based on assumptions of a rigid dam, incompressible water, and a straight dam. Generally, dynamic interaction between the dam and foundation was not considered in evaluating the aforementioned earthquake forces, but in stress analysis of arch dams the flexibility of the foundation sometimes was recognized through the use of Vogt coefficients (Bureau of Reclamation 1965).

The traditional design criteria required that the compressive stress not exceed one‐fourth of the compressive strength or 1000 psi, and the tensile stress should remain below 150 psi.

As mentioned in Section 1.3.3in the context of gravity dams, the seismic coefficient of 0.1 is much smaller than the ordinates of the pseudo‐acceleration response spectra for intense ground motions ( Figure 1.3.2). Thus the earthquake forces for arch dams also were greatly underestimated in traditional analysis procedures.

The effective earthquake forces on a dam due to horizontal ground motion may be expressed as the product of a seismic coefficient, which varies over the dam surface, and the weight of the dam per unit surface area. The seismic coefficient associated with earthquake forces in the first two modes of vibration of the dam (fundamental symmetric and anti‐symmetric modes of a symmetric dam) varies, as shown in Figure 1.4.1. In contrast, traditional design procedures ignore the vibration properties of the dam and adopt a uniform distribution for the seismic coefficient, resulting in erroneous distribution of lateral forces and hence of stresses in the dam. A dynamic analysis procedure that eliminates such errors is developed in Chapter 8. Including dam–water–foundation interaction, this procedure is shown in Chapter 10to produce seismic response results that are consistent with the motions of two arch dams recorded during earthquakes.

As mentioned in Section 1.3.3, the additional water pressures included in traditional design procedures for gravity dams are unrealistically small and have little influence on the computed stresses and hence on the geometry of the dam that satisfies the design criteria. This observation is equally valid for arch dams because the additional water pressures considered for arch dams are similar to those for gravity dams.

Demonstrated in Chapter 9is the importance of two interaction mechanisms – which are ignored in traditional design – in the dynamics of arch dams. When dam–water interaction and water compressibility are properly considered, hydrodynamic effects result in significant increases in the earthquake‐induced stresses in arch dams, more so than for gravity dams. Similarly, when dam–foundation interaction including foundation mass and radiation damping are properly considered, this interaction mechanism generally has a profound influence on the earthquake‐induced stresses in arch dams just as in the case of gravity dams.

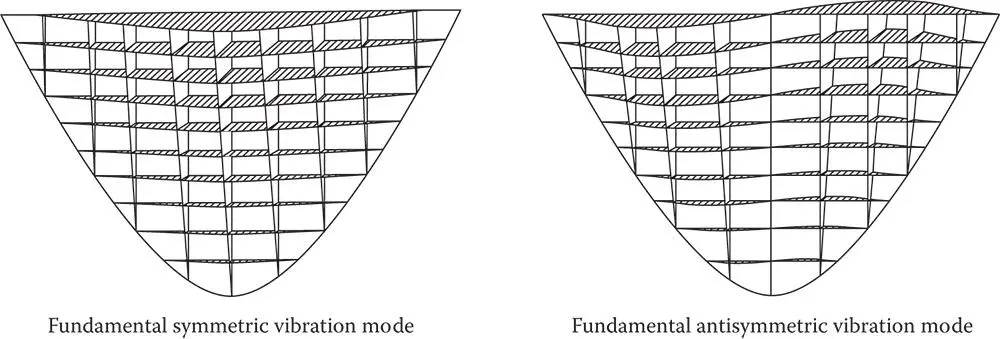
Figure 1.4.1Distribution of seismic coefficients over the dam surface in the first two vibration modes of an arch dam.

Source: Adapted from Bureau of Reclamation (1977).

Traditional design procedures greatly underestimate seismic demands imposed on both arch and gravity dams, as well as the capacity of these structures to resist these demands. The seismic forces associated with the mass of the dam and the hydrodynamic pressures are underestimated, as mentioned earlier. The tensile strength of concrete, which is not insignificant, is essentially ignored in the no‐tension requirement in the design criteria for gravity dams and by the small value allowed for arch dams. A progressive, systematic approach to computation of seismic demands and evaluation of structural capacity is presented in Chapter 12.

Methods for designing dams must be improved in at least two major ways: (i) the tensile strength of concrete should be determined by testing cylindrical cores that are large enough – diameter equal to three or four times the size of the coarse aggregate; and (ii) seismic demands should be computed by dynamic response analysis of the dam–water–foundation system. Development of such analysis procedures is one of the main thrusts of this book.