Anil K. Chopra - Earthquake Engineering for Concrete Dams

Considering all these factors, analytical and computational procedures to determine the response of dam–water–foundation systems subjected to ground shaking are presented in this book. A substructure method for linear analysis of two‐dimensional (2D) models, usually appropriate for gravity dams, is the subject of Chapters 2– 6; and of three‐dimensional (3D) models – required for arch dams, buttress dams, and gravity dams in narrow canyons – is the subject of Chapter 8. The Direct Finite‐Element Method (FEM) for nonlinear analysis of 2D or 3D dam–water–foundation systems is presented in Chapter 11.

Figure 1.2.1Olivenhain Dam, California, USA. Completed in 2003, this is a 318‐ft‐high roller‐compacted concrete dam with a crest length of 2552 ft.

Figure 1.2.2Morrow Point Dam, Colorado, USA, a 465‐ft‐high single‐centered arch dam.

Concrete gravity dams have traditionally been designed and analyzed by very simple procedures (U.S. Army Corps of Engineers 1958; Bureau of Reclamation 1965, 1966). Earthquake effects were treated simply as static forces and were combined with the hydrostatic pressures and gravity loads. In representing the effects of horizontal ground motion – transverse to the axis of the dam – by static lateral forces, neither the dynamic response characteristics of the dam–water–foundation system nor the amplitude and frequency content of earthquake ground motion were recognized. Two types of static lateral forces were included. Forces associated with the weight of the dam were expressed as a product of a seismic coefficient – which was typically constant over the height, with a value between 0.05 to 0.10 – and the weight of the portion of the dam being considered. Water pressures, in addition to the hydrostatic pressure, were specified as the product of the seismic coefficient and a pressure coefficient that was based on assumptions of a rigid dam and incompressible water. Finally, interaction between the dam and the foundation was not considered in computing the aforementioned earthquake forces.

The traditional design criteria required that an ample safety factor be provided against overturning, sliding, and overstressing; in particular, compressive stresses should be less than one‐fourth of the compressive strength. Usually tension was not permitted, and even if it was, the allowable tension was so small that the possibility of cracking of concrete was not considered.

Koyna Dam in India was designed by the traditional static analysis procedure using a seismic coefficient of 0.05. Even though a “no‐tension” criterion was satisfied in the design procedure, as mentioned earlier, the earthquake of December 11, 1967 caused significant horizontal cracks in the upstream and/or downstream faces of a number of the taller non‐overflow monoliths near the elevation at which there is an abrupt change in slope of the downstream face ( Figure 1.1.2).

To understand why the damage occurred, the dynamic response of the tallest non‐overflow monolith to the recorded ground motion was computed assuming linear behavior. The results indicated large tensile stresses on both faces, with the greatest values near the elevation where the slope of the downstream face changes abruptly. These computed stresses (shown in Figure 1.3.1), which exceeded 600 psi on the upstream face and 1000 psi on the downstream face, were about two to three times the estimated tensile strength – 350 psi – of the concrete at that elevation. Hence significant cracking consistent with what was observed after the earthquake could have been anticipated. A similar analysis of the overflow monoliths indicated that cracking should not have occurred there, which is also consistent with the observed behavior.

It is apparent from the preceding discussion that the dynamic stresses that develop in gravity dams bear little resemblance to the results obtained from traditional static design procedures. In the case of Koyna Dam, no tensile stresses were expected when designing the dam for earthquake forces based on a seismic coefficient of 0.05, uniform over the height; however, the earthquake caused significant tensile cracking in the dam. This discrepancy is the result of using too small a seismic coefficient and not recognizing the amplification of acceleration over the height of the dam.

The typical design seismic coefficients, 0.05–0.10, are much smaller than the ordinates of design spectra for intense earthquake motions in the range of vibration periods for concrete gravity dams ( Figure 1.3.2). Note that the seismic base shear coefficient values for dams are similar to those specified for multistory buildings. However, building code design provisions have been based on the premise that buildings should be able to: “(i) resist minor earthquakes without damage; (ii) resist moderate earthquakes without structural damage; and (iii) resist major earthquakes…without collapse but with some structural…damage.” While these may be appropriate design objectives for buildings, major dams should be designed more conservatively, and this intended conservatism is reflected in the no‐tension requirement imposed in traditional methods for designing dams. What the traditional methods fail to recognize, however, is that this requirement must be tied to the dynamic response of the dam that is influenced by its natural vibration periods and modes.

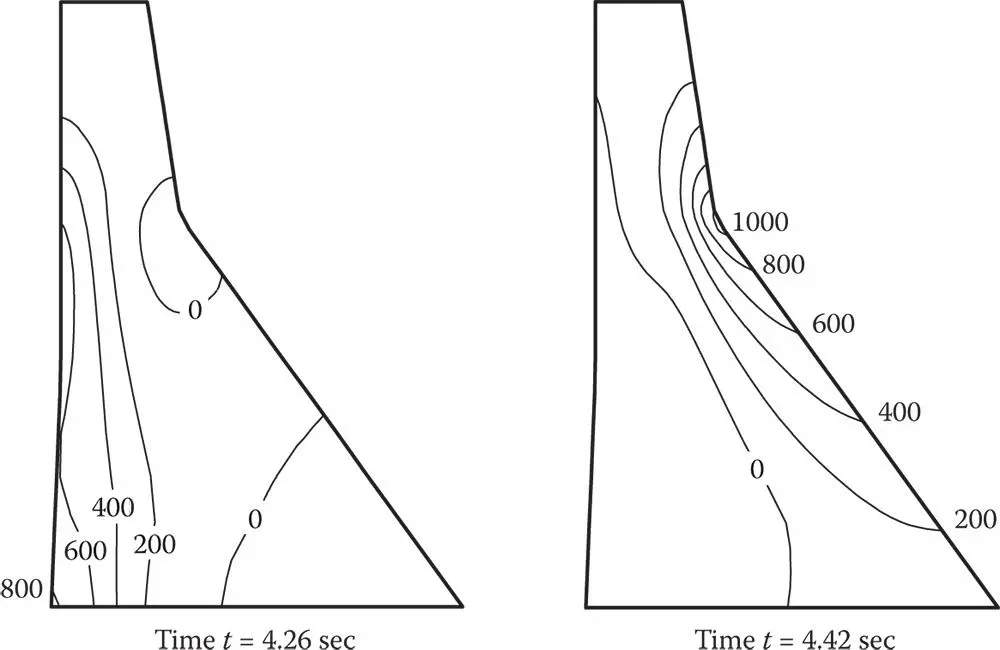
Figure 1.3.1Maximum principal stresses in Koyna Dam at selected time instants due to transverse and vertical components of ground motion recorded during the December 11, 1967 earthquake; initial static stresses are included.

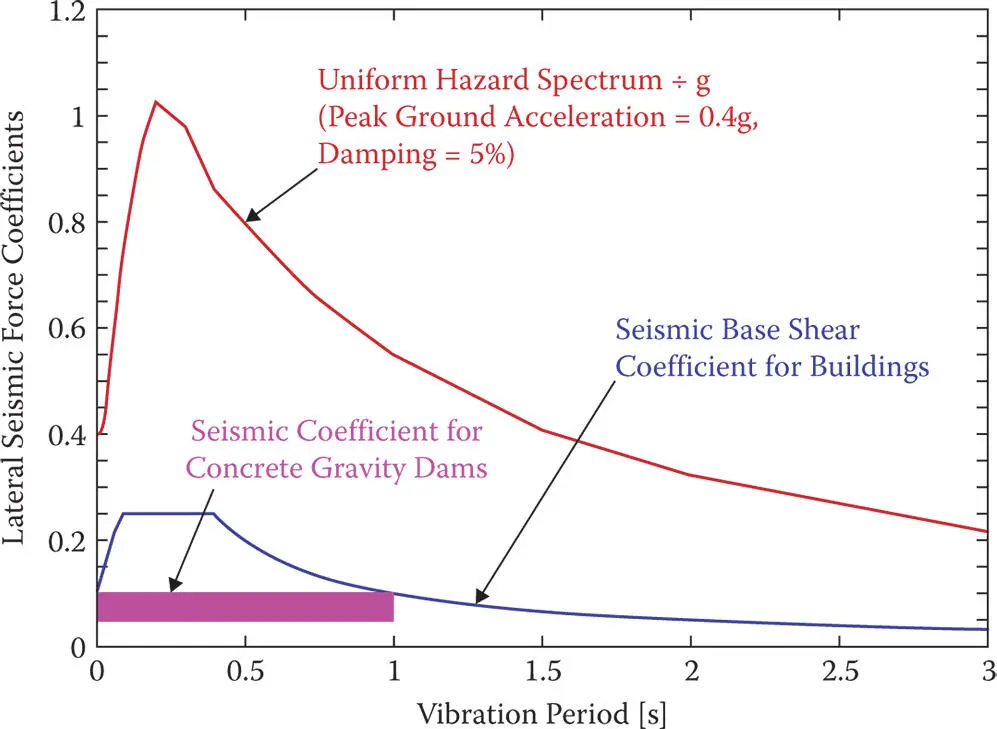
Figure 1.3.2Comparison of uniform hazard spectrum and seismic coefficient for concrete dams and buildings.

Source: Adapted from Chopra (1978).

The effective modal earthquake forces may be expressed as the product of the weight of the dam per unit height and a seismic coefficient; its magnitude depends on the pseudo‐acceleration spectral ordinate at the modal period and its height‐wise distribution depends on the shape of the mode. The response of short‐vibration‐period structures, such as concrete gravity dams, is dominated by the fundamental mode of vibration, and the seismic coefficient varies over the dam height, as shown schematically in Figure 1.3.3b. In contrast, traditional analysis and design procedures ignore the dynamic amplification of response, as reflected in the response spectrum and the shape of the mode, and adopt a uniform distribution for the design coefficient ( Figure 1.3.3a), resulting in an erroneous distribution of lateral forces and hence of stresses in the dam. The implications of these errors will be discussed in Chapter 7.

To eliminate these errors, it is imperative to consider the dynamics of the system subjected to realistic ground motions in estimating the earthquake response of concrete dams. In Chapters 2– 6, such procedures for dynamic analysis of 2D models of gravity dams are developed. In Chapter 7, responses computed by these procedures are demonstrated to be consistent with motions of a gravity dam recorded during an earthquake and with the earthquake performance of Koyna (gravity) Dam.