Table 2.3.2Frequency distribution for the data in Table 2.3.1.
|
|
Frequency |
Cumulative |
|
Cumulative |
| Categories |
Tally |
or count |
frequency |
Percentage |
percentage |
| 1 |
///// ///// ///// ///// ///// /// |
28 |
28 |
25.45 |
25.45 |
| 2 |
///// ///// ///// ///// ///// / |
26 |
54 |
23.64 |
49.09 |
| 3 |
///// ///// ///// ///// |
20 |
74 |
18.18 |
67.27 |
| 4 |
///// ///// ///// / |
16 |
90 |
14.55 |
81.82 |
| 5 |
///// ///// ///// ///// |
20 |
110 |
18.18 |
100.00 |
| Total |
|
110 |
|
100.00 |
|
Interestingly, we can put technology to work on data in Table 2.3.1to produce Table 2.3.2.
Example 2.3.2(Industrial revenue) Using MINITAB and R, construct a frequency distribution table for the data in Table 2.3.1.
1 Enter the data in column C1 of the Worksheet Window and name it Categories.
2 From the Menu bar, select Stat Tables Tally Individual Variables
3 In this dialog box, enter C1 in the box under Variables.
4 Check all the boxes under Display and click OK.
5 The frequency distribution table as shown below appears in the Session window.
This frequency distribution table may also be obtained by using R as follows:
USING R
R has built in ‘table()’ function that can be used to get the basic frequency distribution of categorical data. To get the cumulative frequencies, we can apply built in ‘cumsum()’ function to tabulated frequency data. Then using the ‘cbind()’ function we combine categories, frequencies, cumulative frequencies, and cumulative percentages to build the final distribution table. In addition, we can use the ‘colnames()’ function to name the columns of the final table as needed. The task can be completed running the following R code in R Console window.
#Assign given data to the variable data data = c(4,3,5,3,4,1,2,3,4,3,1,5,3,4,2,1,1,4,5,3,2,5,2,5,2,1,2,3,3,2, 1,5,3,2,1,1,2,1,2,4,5,3,5,1,3,1,2,1,4,1,4,5,4,1,1,2,4,1,4,1,2,4,3,4,1, 4,1,4,1,2,1,5,3,1,5,2,1,2,3,1,2,2,1,1,2,1,5,3,2,5,5,2,5,3,5,2,3,2,3,5, 2,3,5,5,2,3,2,5,1,4) #To get frequencies data.freq = table(data) #To combine necessary columns freq.dist = cbind(data.freq, cumsum(data.freq), 100*cumsum(data.freq)/sum(data.freq)) #To name the table columns colnames(freq.dist) = c(‘Frequency’,‘Cum.Frequency’,‘Cum Percentage’) freq.dist #R output
|
Frequency |
Cum.Frequency |
Cum Percentage |
| 1 |
28.00 |
28.00 |
25.45 |
| 2 |
26.00 |
54.00 |
49.09 |
| 3 |
20.00 |
74.00 |
67.27 |
| 4 |
16.00 |
90.00 |
81.82 |
| 5 |
20.00 |
110.00 |
100.00 |
Note that sometimes a quantitative data set is such that it consists of only a few distinct observations that occur repeatedly. These kind of data are usually summarized in the same manner as the categorical data. The categories are represented by the distinct observations. We illustrate this scenario with the following example.
Example 2.3.3(Hospital data) The following data show the number of coronary artery bypass graft surgeries performed at a hospital in a 24‐hour period for each of the last 50 days. Bypass surgeries are usually performed when a patient has multiple blockages or when the left main coronary artery is blocked. Construct a frequency distribution table for these data.
| 1 |
2 |
1 |
5 |
4 |
2 |
3 |
1 |
5 |
4 |
3 |
4 |
6 |
2 |
3 |
3 |
2 |
2 |
3 |
5 |
2 |
5 |
3 |
4 |
3 |
| 1 |
3 |
2 |
2 |
4 |
2 |
6 |
1 |
2 |
6 |
6 |
1 |
4 |
5 |
4 |
1 |
4 |
2 |
1 |
2 |
5 |
2 |
2 |
4 |
3 |
Solution:In this example, the variable of interest is the number of bypass surgeries performed at a hospital in a period of 24 hours. Now, following the discussion in Example 2.3.1, we can see that the frequency distribution table for the data in this example is as shown in Table 2.3.3. Frequency distribution table defined by using a single numerical value is usually called a single‐valued frequency distribution table.
Table 2.3.3Frequency distribution table for the hospital data.
|
|
Frequency |
Cumulative |
|
Cumulative |
| Categories |
Tally |
or count |
frequency |
Percentage |
percentage |
| 1 |
///// /// |
8 |
8 |
16.00 |
16.00 |
| 2 |
///// ///// //// |
14 |
22 |
28.00 |
44.00 |
| 3 |
///// //// |
9 |
31 |
18.00 |
62.00 |
| 4 |
///// //// |
9 |
40 |
18.00 |
80.00 |
| 5 |
///// / |
6 |
46 |
12.00 |
92.00 |
| 6 |
//// |
4 |
50 |
8.00 |
100.00 |
| Total |
|
50 |
|
100.00 |
|
So far, we have discussed frequency distribution tables for qualitative data and quantitative data that can be treated as qualitative data. In this section, we discuss frequency distribution tables for quantitative data.
Let 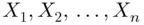 be a set of quantitative data values. To construct a frequency distribution table for this data set, we follow the steps given below.
be a set of quantitative data values. To construct a frequency distribution table for this data set, we follow the steps given below.
1 Step 1. Find the range of the data that is defined as(2.3.1)
2 Step 2. Divide the data set into an appropriate number of classes. The classes are also sometimes called categories, cells, or bins. There are no hard and fast rules to determine the number of classes. As a rule, the number of classes, say , should be somewhere between 5 and 20. However, Sturges's formula is often used, given by (2.3.2)or (2.3.3)where is the total number of data points in a given data set and log denotes the log to base 10. The result often gives a good estimate for an appropriate number of intervals. Note that since , the number of classes, should always be a whole number, the reader may have to round up or down the value of obtained when using either equation (2.3.2) or (2.3.3).
3 Step 3. Determine the width of classes as follows: (2.3.4)The class width should always be a number that is easy to work with, preferably a whole number. Furthermore, this number should be obtained only by rounding up (never by rounding down) the value obtained when using equation (2.3.4).
4 Step 4. Finally, preparing the frequency distribution table is achieved by assigning each data point to an appropriate class. While assigning these data points to a class, one must be particularly careful to ensure that each data point be assigned to one, and only one, class and that the whole set of data is included in the table. Another important point is that the class at the lowest end of the scale must begin at a number that is less than or equal to the smallest data point and that the class at the highest end of the scale must end with a number that is greater than or equal to the largest data point in the data set.
Читать дальше

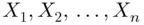 be a set of quantitative data values. To construct a frequency distribution table for this data set, we follow the steps given below.
be a set of quantitative data values. To construct a frequency distribution table for this data set, we follow the steps given below.










