Ordinal data are more informative than nominal data. When the ordering of categories becomes important, the data collected are called ordinal. Examples include companies ranked according to the quality of their product, companies ranked based on their annual revenues, the severity of burn types, or stage of cancer among cancer‐afflicted patients. Again, no addition, subtraction, multiplication, or division can be used on ordinal‐type data.
Other examples of ordinal data are represented by geographical regions, say designated as A, B, C, and D for shipping purposes, or preference of vendors who can be called upon for service, or skill ratings of certain workers of a company, or in electronics engineering, the color‐coded resistors, which represent ascending order data.
Interval data are numerical data, more informative than nominal and ordinal data but less informative than ratio data. A typical example of interval data is temperature (in Celsius and Fahrenheit). Arithmetic operations of addition and subtraction are applicable, but multiplication and division are not applicable. For example, the temperature of three consecutive parts A, B, and C during a selected step in a manufacturing process are 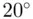 F,
F, 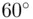 F, and
F, and 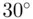 F, respectively. Then we can say the temperature difference between parts A and B is different from the difference between parts B and C. Also we can say that part B is warmer than part A and part C is warmer than part A, but cooler than part B. However, it is physically meaningless to say that part B is three times as warm as part A and twice as warm as part C. Moreover, in interval data, zero does not have the conventional meaning of nothingness; it is just an arbitrary point on the scale of measurement. For instance,
F, respectively. Then we can say the temperature difference between parts A and B is different from the difference between parts B and C. Also we can say that part B is warmer than part A and part C is warmer than part A, but cooler than part B. However, it is physically meaningless to say that part B is three times as warm as part A and twice as warm as part C. Moreover, in interval data, zero does not have the conventional meaning of nothingness; it is just an arbitrary point on the scale of measurement. For instance, 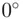 F and
F and 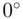 C (=
C (= 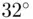 F) have different values, and they are in fact the arbitrary points on different scales of measurements. Other examples of interval data are year in which a part is produced, students' numeric grades on a test, and date of birth.
F) have different values, and they are in fact the arbitrary points on different scales of measurements. Other examples of interval data are year in which a part is produced, students' numeric grades on a test, and date of birth.
Ratio data are also numerical data that have the potential to produce the most meaningful information of all data types. All arithmetic operations are applicable on this type of data. Numerous examples of this type of data exist, such as height, weight, length of rods, diameter of a ball bearing, RPM of a motor, number of employees in a company, hourly wages, and annual growth rate of a company. In ratio data, the number zero equates to nothingness. In other words, the number zero means absence of the characteristics of interest.
PRACTICE PROBLEMS FOR SECTIONS 2.1 AND 2.2
1 Describe briefly the difference between a sample and a population. Give an example of a population and a sample.
2 Describe the difference between descriptive statistics and inferential statistics.
3 A university professor is interested in knowing the average GPA of a graduating class. The professor decided to record the GPA of only those students who were in his/her class during the last semester before graduation. Using this information (the data), the professor estimates the average GPA of the graduating class using the average of the GPAs he/she collected. Describe the following:Population of interestSample collected by the professorThe variable of interest
4 Describe whether each of the following scenarios would result in qualitative or quantitative data:Time needed to finish a project by a technicianNumber of days of stay in a hospital by a patient after bypass surgeryAverage number of cars passing through a toll booth each dayTypes of beverages served by a restaurantSize of a rod used in a projectCondition of a home for sale (excellent, good, fair, bad)Heights of basketball playersDose of medication prescribed by a physician to his/her patientsRecorded temperatures of a tourist place during the month of JanuaryAges of persons waiting in a physician's officeSpeed of a vehicle crossing George Washington Bridge in New YorkAmount of interest reported in a tax returnSizes of cars available at a rental company (full, medium, compact, small)Manufacturers of cars parked in a parking lot
5 Referring to Problem 4, classify the data in each case as nominal, ordinal, interval, or ratio.
6 A consumer protection agency conducts opinion polls to determine the quality (excellent, good, fair, bad) of products imported from an Asian country. Suppose that the agency conducted a poll in which 1000 randomly selected individuals were contacted by telephone.What is the population of interest?What is the sample?Classify the variable of interest as nominal, ordinal, interval, or ratio.
2.3 Frequency Distribution Tables for Qualitative and Quantitative Data
In statistical applications, we often encounter large quantities of messy data. To gain insight into the nature of the data, we often organize and summarize the data by constructing a table called a frequency distribution table . In any statistical application (as noted in Section 2.2), we can have data that are either qualitative or quantitative. Qualitative and quantitative are sometimes referred to as categorical or numerical data, respectively. In this section, we discuss the construction of a frequency distribution table when the data are qualitative or quantitative.
A frequency distribution table for qualitative data consists of two or more categories along with the numbers of the data that belong to each category. The number of data belonging to any particular category is called the frequency or count of that category. We illustrate the construction of a frequency distribution table when the data are qualitative with the following example.
Example 2.3.1(Industrial revenue) Consider a random sample of 110 small to midsize companies located in the midwestern region of the United States, and classify them according to their annual revenues (in millions of dollars). Then construct a frequency distribution table for the data obtained by this classification.
Solution:We classify the annual revenues into five categories as follows: Under 250, 250–under 500, 500–under 750, 750–under 1000, 1000 or more. Then the data collected can be represented as shown in Table 2.3.1, where we have used the labels 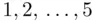 for the above categories.
for the above categories.
Table 2.3.1Annual revenues of 110 small to midsize companies located in mid‐western region of the United States.
| 1 |
4 |
3 |
5 |
3 |
4 |
1 |
2 |
3 |
4 |
3 |
1 |
5 |
3 |
4 |
2 |
1 |
1 |
4 |
5 |
3 |
2 |
5 |
2 |
5 |
2 |
1 |
2 |
3 |
| 3 |
2 |
1 |
2 |
5 |
3 |
2 |
1 |
1 |
2 |
1 |
2 |
4 |
5 |
3 |
5 |
1 |
3 |
1 |
2 |
1 |
4 |
1 |
4 |
5 |
4 |
1 |
1 |
2 |
| 4 |
1 |
4 |
1 |
2 |
4 |
3 |
3 |
4 |
1 |
4 |
1 |
4 |
1 |
2 |
1 |
5 |
3 |
1 |
5 |
2 |
1 |
2 |
3 |
1 |
2 |
2 |
1 |
1 |
| 2 |
1 |
5 |
3 |
2 |
5 |
5 |
2 |
5 |
4 |
3 |
5 |
2 |
3 |
2 |
3 |
5 |
2 |
3 |
5 |
5 |
2 |
3 |
2 |
5 |
1 |
4 |
|
|
After tallying the data, we find that of the 110 companies, 28 belong in the first category, 26 in the second category, 20 in the third category, 16 in the fourth category, and 20 in the last category. Thus, a frequency distribution table for the data in Table 2.3.1is as shown in Table 2.3.2.
Читать дальше

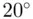 F,
F, 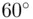 F, and
F, and 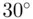 F, respectively. Then we can say the temperature difference between parts A and B is different from the difference between parts B and C. Also we can say that part B is warmer than part A and part C is warmer than part A, but cooler than part B. However, it is physically meaningless to say that part B is three times as warm as part A and twice as warm as part C. Moreover, in interval data, zero does not have the conventional meaning of nothingness; it is just an arbitrary point on the scale of measurement. For instance,
F, respectively. Then we can say the temperature difference between parts A and B is different from the difference between parts B and C. Also we can say that part B is warmer than part A and part C is warmer than part A, but cooler than part B. However, it is physically meaningless to say that part B is three times as warm as part A and twice as warm as part C. Moreover, in interval data, zero does not have the conventional meaning of nothingness; it is just an arbitrary point on the scale of measurement. For instance, 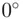 F and
F and 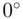 C (=
C (= 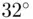 F) have different values, and they are in fact the arbitrary points on different scales of measurements. Other examples of interval data are year in which a part is produced, students' numeric grades on a test, and date of birth.
F) have different values, and they are in fact the arbitrary points on different scales of measurements. Other examples of interval data are year in which a part is produced, students' numeric grades on a test, and date of birth.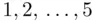 for the above categories.
for the above categories.










