A list of all sampling units is called the sampling frame .
The most commonly used sample design is the simple random sampling design , which consists of selecting 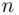 (sample size) sampling units in such a way that each sampling unit has the same chance of being selected. If, however, the population is finite of size
(sample size) sampling units in such a way that each sampling unit has the same chance of being selected. If, however, the population is finite of size 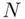 , say, then the simple random sampling design may be defined as selecting
, say, then the simple random sampling design may be defined as selecting  sampling units in such a way that each possible sample of size
sampling units in such a way that each possible sample of size 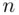 has the same chance of being selected. The number of such samples of size
has the same chance of being selected. The number of such samples of size  that may be formed from a finite population of size
that may be formed from a finite population of size  is discussed in Section 3.4.3.
is discussed in Section 3.4.3.
Example 2.1.1(Simple random sampling) Suppose that an engineer wants to take a sample of machine parts manufactured during a shift at a given plant. Since the parts from which the engineer wants to take the sample are manufactured during the same shift at the same plant, it is quite safe to assume that all parts are representative. Hence in this case, a simple random sampling design should be appropriate.
The second sampling design is the stratified random sampling design , which may give improved results for the same amount of money spent for simple random sampling. However, a stratified random sampling design is appropriate when a population can be divided into various nonoverlapping groups called strata . The sampling units in each stratum are similar but differ from stratum to stratum. Each stratum is treated as a subpopulation, and a simple random sample is taken from each of these subpopulations or strata.
In the manufacturing world, this type of sampling situation arises quite often. For instance, in Example 2.1.1, if the sample is taken from a population of parts manufactured either in different plants or in different shifts, then stratified random sampling can be more appropriate than simple random sampling. In addition, there is the advantage of administrative convenience. For example, if the machine parts are manufactured in plants located in different parts of the country, then stratified random sampling can be beneficial. Often, each plant (stratum) has a sampling department that can conduct the random sampling within each plant. In order to obtain best results in this case, the sampling departments in all the plants need to communicate with one another before sampling in order to ensure that the same sampling norms are followed. Another example of stratified random sampling in manufacturing occurs when samples are taken of products that are produced in different batches; here, products produced in different batches constitute the different strata.
A third kind of sampling design is systematic random sampling . The systematic random sampling procedure is the easiest one. This sampling scheme is particularly useful in manufacturing processes, when the sampling is done from a continuously operating assembly line. Under this scheme, a first item is selected randomly and thereafter every  th
th 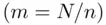 item manufactured is selected until we have a sample of the desired size (
item manufactured is selected until we have a sample of the desired size ( 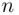 ). Systematic sampling is not only easy to employ but, under certain conditions, is also more precise than simple random sampling.
). Systematic sampling is not only easy to employ but, under certain conditions, is also more precise than simple random sampling.
The fourth and last sampling design is cluster random sampling . In cluster sampling, each sampling unit is a group of smaller units. In the manufacturing environment, this sampling scheme is particularly useful since it is difficult to prepare a list of each part that constitutes a frame. On the other hand, it may be easier to prepare a list of boxes in which each box contains many parts. Thus, in this case, a cluster random sample is merely a simple random sample of these boxes. Another advantage of cluster sampling is that by selecting a simple random sample of only a few clusters, we can in fact have quite a large sample of smaller units. Such sampling is achieved at minimum cost, since both preparing the frame and taking the sample are much more economical. In preparing any frame, we must define precisely the characteristic of interest or variable, where a variable may be defined as follows:
A variable is a characteristic of interest that may take different values for different elements.
For example, an instructor is interested in finding the ages, heights, weights, GPA, gender, and family incomes of all the students in her engineering class. Thus, in this example, the variables (characteristics of interest) are ages, heights, weights, GPA, gender, and family incomes.
2.2 Classification of Various Types of Data
In practice, it is common to collect a large amount of nonnumerical and/or numerical data on a daily basis. For example, we may collect data concerning customer satisfaction, comments of employees, or perceptions of suppliers. Or we may track the number of employees in various departments of a company or check weekly production volume in units produced and sales dollars per unit of time, and so on. All the data collected, however, cannot be treated the same way as there are differences in types of data. Accordingly, statistical data can normally be divided into two major categories:
Qualitative
Quantitative
Each of these categories can be further subdivided into two subcategories each. The two subcategories of qualitative data are nominal and ordinal , whereas the two subcategories of quantitative data are interval and ratio . We may summarize this classification of statistical data as in Figure 2.2.1.
The classification of data as nominal, ordinal, interval, and ratio is arranged in the order of the amount of information they can provide. Nominal data provide minimum information, whereas ratio data provide maximum information.

Figure 2.2.1Classifications of statistical data.
As previously mentioned, nominal data contain the smallest amount of information. Only symbols are used to label categories of a population. For example, production part numbers with a 2003 prefix are nominal data, wherein the 2003 prefix indicates only that the parts were produced in 2003 (in this case, the year 2003 serves as the category). No arithmetic operation, such as addition, subtraction, multiplication, or division, can be performed on numbers representing nominal data. As another example, jersey numbers of baseball, football, or soccer players are nominal. Thus, adding any two jersey numbers and comparing with another number makes no sense. Other examples of nominal data are ID numbers of workers, account numbers used by a financial institution, ZIP codes, telephone numbers, sex, or color.
Читать дальше

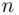 (sample size) sampling units in such a way that each sampling unit has the same chance of being selected. If, however, the population is finite of size
(sample size) sampling units in such a way that each sampling unit has the same chance of being selected. If, however, the population is finite of size 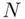 , say, then the simple random sampling design may be defined as selecting
, say, then the simple random sampling design may be defined as selecting  sampling units in such a way that each possible sample of size
sampling units in such a way that each possible sample of size 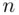 has the same chance of being selected. The number of such samples of size
has the same chance of being selected. The number of such samples of size  that may be formed from a finite population of size
that may be formed from a finite population of size  is discussed in Section 3.4.3.
is discussed in Section 3.4.3. th
th 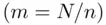 item manufactured is selected until we have a sample of the desired size (
item manufactured is selected until we have a sample of the desired size ( 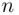 ). Systematic sampling is not only easy to employ but, under certain conditions, is also more precise than simple random sampling.
). Systematic sampling is not only easy to employ but, under certain conditions, is also more precise than simple random sampling.











