Chapter 9deals with the important topic of statistical tests of hypotheses and discusses test procedures when concerned with the population means, population variance, and population proportion for one and two populations. Methods of testing hypotheses using the confidence intervals studied in Chapter 8are also presented.
Chapter 10gives an introduction to the theory of reliability. Methods of estimation and hypothesis testing using the exponential and Weibull distributions are presented.
In Chapter 11, we introduce the topic of data mining. It includes concepts of big data and starting steps in data mining. Classification, machine learning, and inference versus prediction are also discussed.
In Chapter 12, we introduce topic of cluster analysis. Clustering concepts and similarity measures are introduced. The hierarchical and nonhierarchical clustering techniques and model‐based clustering methods are discussed in detail.
Chapter 13is concerned with the chi‐square goodness‐of‐fit test, which is used to test whether a set of sample data support the hypothesis that the sampled population follows some specified probability model. In addition, we apply the chi‐square goodness‐of‐fit test for testing hypotheses of independence and homogeneity. These tests involve methods of comparing observed frequencies with those that are expected if a certain hypothesis is true.
Chapter 14gives a brief look at tests known as “nonparametric tests,” which are used when the assumption about the underlying distribution having some specified parametric form cannot be made.
Chapter 15introduces an important topic of applied statistics: simple linear regression analysis. Linear regression analysis is frequently used by engineers, social scientists, health researchers, and biological scientists. This statistical technique explores the relation between two variables so that one variable can be predicted from the other. In this chapter, we discuss the least squares method for estimating the simple linear regression model, called the fitting of this regression model. Also, we discuss how to perform a residual analysis, which is used to check the adequacy of the regression model, and study certain transformations that are used when the model is not adequate.
Chapter 16extends the results of Chapter 15to multiple linear regressions. Similar to the simple linear regression model, multiple linear regression analysis is widely used. It provides statistical techniques that explore the relations among more than two variables, so that one variable can be predicted from the use of the other variables. In this chapter, we give a discussion of multiple linear regression, including the matrix approach. Finally, a brief discussion of logistic regression is given.
In Chapter 17, we introduce the design and analysis of experiments using one, two, or more factors. Designs for eliminating the effects of one or two nuisance variables along with a method of estimating one or more missing observations are given. We include two nonparametric tests, the Kruskal–Wallis and the Friedman test, for analyzing one‐way and randomized complete block designs. Finally, models with fixed effects, mixed effects, and random effects are also discussed.
Chapter 18introduces a special class of designs, the so‐called 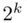 factorial designs. These designs are widely used in various industrial and scientific applications. An extensive discussion of unreplicated
factorial designs. These designs are widely used in various industrial and scientific applications. An extensive discussion of unreplicated 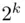 factorial designs, blocking of
factorial designs, blocking of 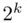 factorial designs, confounding in the
factorial designs, confounding in the 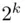 factorial designs, and Yates's algorithm for the
factorial designs, and Yates's algorithm for the  factorial designs is also included. We also devote a section to fractional factorial designs, discussing one‐half and one‐quarter replications of
factorial designs is also included. We also devote a section to fractional factorial designs, discussing one‐half and one‐quarter replications of 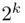 factorial designs.
factorial designs.
In Chapter 19, we introduce the topic of response surface methodology (RSM). First‐order and second‐order designs used in RSM are discussed. Methods of determining optimum or near optimum points using the “method of steepest ascent” and the analysis of a fitted second‐order response surface are also presented.
Chapters 20and 21are devoted to control charts for variables and attributes used in phase I and phase II of a process. “Phase I” refers to the initial stage of a new process, and “phase II” refers to a matured process. Control charts are used to determine whether a process involving manufacturing or service is “under statistical control” on the basis of information contained in a sequence of small samples of items of interest. Due to lack of space, these two chapters are not included in the text but is available for download from the book website: www.wiley.com/college/gupta/statistics2e.
All the chapters are supported by three popular statistical software packages, MINITAB, R, and JMP. The MINITAB and R are fully integrated into the text of each chapter, whereas JMP is given in an independent section, which is not included in the text but is available for download from the book website: www.wiley.com/college/gupta/statistics2e. Frequently, we use the same examples for the discussion of JMP as are used in the discussion of MINITAB and R. For the use of each of these software packages, no prior knowledge is assumed, since we give each step, from entering the data to the final analysis of such data under investigation. Finally, a section of case studies is included in almost all the chapters.
Part I Fundamentals of Probability and Statistics
Chapter 2 Describing Data Graphically and Numerically
The focus of this chapter is a discussion of methods for describing sets of data.
Basic concepts of a population and various types of sampling designs
Classification of the types of data
Organizing and summarizing qualitative and quantitative data
Describing qualitative and quantitative data graphically
Determining measures of centrality and measures of dispersion for a set of raw data
Determining measures of centrality and measures of dispersion for grouped data
Determining measures of relative position
Constructing a box whisker plot and its use in data analysis
Determining measures of association
Using statistical packages MINITAB, R, and JMP
After studying this chapter, the reader will be able to do the following:
Select an appropriate sampling design for data collection.
Identify suitable variables in a problem and determine the level of measurement.
Organize, summarize, present, and interpret the data.
Identify the difference between a parameter and a statistic.
Calculate measures of the data such as mean, mode, median, variance, standard deviation, coefficient of variation, and measure of association and interpret them.
Identify outliers if they are present in the data.
Apply the statistical packages MINITAB, R, and JMP to analyze various sets of data.
2.1 Getting Started with Statistics
Читать дальше

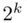 factorial designs. These designs are widely used in various industrial and scientific applications. An extensive discussion of unreplicated
factorial designs. These designs are widely used in various industrial and scientific applications. An extensive discussion of unreplicated 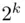 factorial designs, blocking of
factorial designs, blocking of 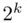 factorial designs, confounding in the
factorial designs, confounding in the 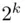 factorial designs, and Yates's algorithm for the
factorial designs, and Yates's algorithm for the  factorial designs is also included. We also devote a section to fractional factorial designs, discussing one‐half and one‐quarter replications of
factorial designs is also included. We also devote a section to fractional factorial designs, discussing one‐half and one‐quarter replications of 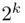 factorial designs.
factorial designs.










