A third experiment, using stainless steel collar screens of two mesh sizes, similar to that attempted in phase b, was performed with the same collar screen mesh size, collar screen speed (rpm), and flow rate (gpm) used before.
In this phase, with a stainless steel collar screen, high removal rates y were possible for eight sets of conditions for the factors just mentioned. However, these high y values were obtained with retreated flow z at undesirably high values (before, they had been too low). The objective was to get reasonably small values for z , but not so small as to make shoveling necessary; values between 5% and 20% were desirable. It was believed that by varying flow rate and speed of rotation of the collar screen, this objective could be achieved without sacrificing solid removal.
Again, using a stainless steel collar screen, another experiment, with two factors, namely collar screen speed (rpm) and flow rate (gpm),set at two levels each, was run. This time, high values of solid removal were maintained, but unfortunately, flow retreated values were even higher than before.
It was now conjectured that intermittent back washing could overcome the difficulties. This procedure was now introduced with influent flow rate and collar screen mesh varied.
The results of this experiment lead to a removal efficiency of  with a retreated flow of only
with a retreated flow of only 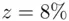 . This was regarded as a satisfactory and practical solution, and the investigation was terminated at that point.
. This was regarded as a satisfactory and practical solution, and the investigation was terminated at that point.
For detailed analysis of this experiment, the reader should refer to Box et al. (1978, p. 354). Of course, these types of experiments and their analyses are discussed in this text (see Chapter 18).
The purpose of a sample survey is to make inferences about certain characteristics of a population from which samples are drawn. The inferences to be made for a population usually entails the estimation of population parameters, such as the population total, the mean, or the population proportion of a certain characteristic of interest. In any sample survey, a clear statement of its objective is very important. Without a clear statement about the objectives, it is very easy to miss pertinent information while planning the survey that can cause difficulties at the end of the study.
In any sample survey, only relevant information should be collected. Sometimes trying to collect too much information may become very confusing and consequently hinder the determination of the final goal. Moreover, collecting information in sample surveys costs money, so that the interested party must determine which and how much information should be obtained. For example, it is important to describe how much precision in the final results is desired. Too little information may prevent obtaining good estimates with desired precision, while too much information may not be needed and may unnecessarily cost too much money. One way to avoid such problems is to select an appropriate method of sampling the population. In other words, the sample survey needs to be appropriately designed. A brief discussion of such designs is given in Chapter 2. For more details on these designs, the reader may refer to Cochran (1977), Sukhatme and Sukhatme (1970), or Scheaffer et al. (2006).
1.3 An Observational Study
An observational study is one that does not involve any experimental studies. Consequently, observational studies do not control any variables. For example, a realtor wishes to appraise a house value. All the data used for this purpose are observational data. Many psychiatric studies involve observational data.
Frequently, in fitting a regression model (see Chapters 15and 16), we use observational data. Similarly, in quality control (see Chapters 20and 21), most of the data used in studying control charts for attributes are observational data. Note that control charts for attributes usually do not provide any cause‐and‐effect relationships. This is because observational data give us very limited information about cause‐and‐effect relationships.
As another example, many psychiatric studies involve observational data, and such data do not provide the cause of patient's psychiatric problems. An advantage of observational studies is that they are usually more cost‐effective than experimental studies. The disadvantage of observational studies is that the data may not be as informative as experimental data.
1.4 A Set of Historical Data
Historical data are not collected by the experimenter. The data are made available to him/her.
Many fields of study such as the many branches of business studies, use historical data. A financial advisor for planning purposes uses sets of historical data. Many investment services provide financial data on a company‐by‐company basis.
1.5 A Brief Description of What is Covered in this Book
Data collection is very important since it can greatly influence the final outcome of subsequent data analyses. After collection of the data, it is important to organize, summarize, present the preliminary outcomes, and interpret them. Various types of tables and graphs that summarize the data are presented in Chapter 2. Also in that chapter, we give some methods used to determine certain quantities, called statistics , which are used to summarize some of the key properties of the data.
The basic principles of probability are necessary to study various probability distributions. We present the basic principles of elementary probability theory in Chapter 3. Probability distributions are fundamental in the development of the various techniques of statistical inference. The concept of random variables is also discussed in Chapter 3.
Chapters 4and 5are devoted to some of the important discrete distributions, continuous distributions, and their moment‐generating functions. In addition, we study in Chapter 5some special distributions that are used in reliability theory.
In Chapter 6, we study joint distributions of two or more discrete and continuous random variables and their moment‐generating functions. Included in Chapter 6is the study of the bivariate normal distribution.
Chapter 7is devoted to the probability distributions of some sample statistics, such as the sample mean, sample proportions, and sample variance. In this chapter, we also study a fundamental result of probability theory, known as the Central Limit Theorem. This theorem can be used to approximate the probability distribution of the sample mean when the sample size is large. In this chapter, we also study some sampling distributions of some sample statistics for the special case in which the population distribution is the so‐called normal distribution. In addition, we present probability distributions of various “order statistics,” such as the largest element in a sample, smallest element in a sample, and sample median.
Chapter 8discusses the use of sample data for estimating the unknown population parameters of interest, such as the population mean, population variance, and population proportion. Chapter 8also discusses the methods of estimating the difference of two population means, the difference of two population proportions, and the ratio of two population variances and standard deviations. Two types of estimators are included, namely point estimators and interval estimators (confidence intervals).
Читать дальше

 with a retreated flow of only
with a retreated flow of only 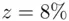 . This was regarded as a satisfactory and practical solution, and the investigation was terminated at that point.
. This was regarded as a satisfactory and practical solution, and the investigation was terminated at that point.










