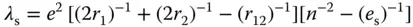Shunichi Fukuzumi - Electron Transfer

When the magnitude of the driving force of electron transfer becomes the same as the reorganization energy (−Δ G ET= λ ), the electron‐transfer rate reaches a maximum and is basically controlled by the magnitude of electronic coupling ( V ) between the donor and acceptor moieties ( Eq. (2.1)). Upon passing this thermodynamic maximum, the highly exothermic region of the parabola (−Δ G ET> λ ) is entered, in which an additional increase of the driving force results in an actual slowdown of the electron‐transfer rate, due to an increasingly poor vibrational overlap of the product and reactant wave functions. This highly exergonic range is generally referred to as the Marcus inverted region [6–8,28,29]. In such a case, the magnitude of the reorganization energy is the key parameter to control the electron‐transfer process. The smaller the reorganization energy, the faster is the forward photoinduced charge‐separation (CS) process, but the charge‐recombination (CR) process becomes slower when the driving force for back electron transfer (–Δ G ET) is larger than the reorganization energy ( λ ) of electron transfer as shown in Figure 2.1. Among the key parameters that govern electron‐transfer reactions ( V , Δ G ET, and λ ), the reorganization energy ( λ ) imposes the most important impact. The primary electron‐transfer processes of photosynthesis are, for example, characterized by an extremely small reorganization energy ( λ ∼ 0.2 eV), attained by the protein environment. This aspect is essential to achieving ultrafast charge separation and retarding the energy‐wasting charge recombination, which is highly exergonic (−Δ G = 1.2 eV) [11–15]. Thus, the components of artificial photosynthesis, which are not necessarily natural components in photosynthesis, must have small λ values of electron transfer.

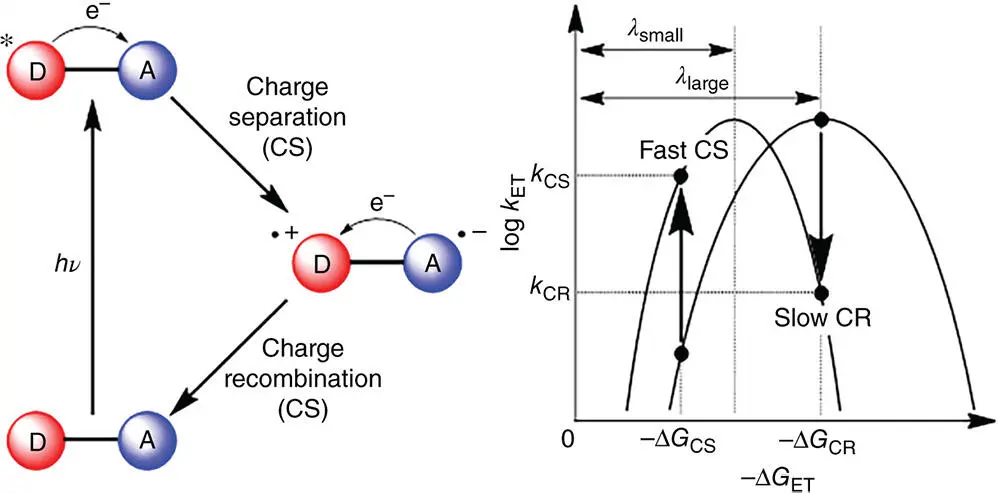
Figure 2.1(a) Schematic diagram of photoinduced electron transfer of an electron donor–acceptor (D–A) dyad. (b) Driving force dependence of log k ETwith different λ values (for the meaning of λ , see text).

The first candidates of artificial photosynthetic reaction centers are porphyrins, which have been involved in a number of important biological electron‐transfer systems including the primary photochemical reactions of chlorophylls in the photosynthetic reaction centers. Porphyrins contain an extensively conjugated two‐dimensional π‐system and are thereby suitable for efficient electron transfer, because the uptake or release of electrons results in minimal structural and solvation change upon electron transfer, resulting in a small λ value of electron transfer [30]. In addition, rich and extensive absorption features of porphyrinoid systems guarantee increased absorption cross sections and efficient use of the solar spectrum [30]. In contrast with the two‐dimensional porphyrin π‐system, fullerenes contain an extensively conjugated three‐dimensional π‐system [31]. Electron transfer to C 60is highly efficient because of the minimal changes of structure and solvation associated with the electron‐transfer reduction [31–33]. Thus, a series of porphyrin–fullerene linked molecules have been designed and synthesized to mimic the charge‐separation processes in the photosynthetic reaction center, starting from a zinc porphyrin–C 60dyad (ZnP–C 60), a ferrocene–zinc porphpyrin–C 60triad (Fc–ZnP–C 60), a zinc porphyrin‐free base porphyrin–C 60triad, up to a tetrad (Fc–ZnP–H 2P–C 60) [34–39].

The driving force dependence of the electron‐transfer rate constants ( k ET) of these dyad, triad, and tetrad molecules for CS and CR processes is shown in Figure 3.1, where log k ETis plotted against the driving force (−Δ G ET) [39]. The lines in Figure 3.1represent the best fit to Eq. (2.1) (ZnP–C 60: λ = 0.66 eV, V = 3.9 cm −1; Fc–ZnP–C 60, Fc–H 2P–C 60, and ZnP–H 2P–C 60: λ = 1.09 eV, V = 0.019 cm −1; Fc–ZnP–H 2P–C 60: λ = 1.32 eV, V = 0.00017 cm −1) [39]. The λ ‐value increases, whereas the V value decreases with increasing edge‐to‐edge distance in the order of the dyad ( R ee= 11.9 Å), the triad ( R ee= 30.3 Å), and the tetrad ( R ee= 48.9 Å). Such an increase in the λ value with increasing distance results from an increase in the solvent reorganization energy ( λ s), because the λ svalue is known to increase with increasing distance between an electron donor and an acceptor as given by Eq. (3.1):

( 3.1)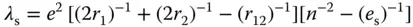

where r 1and r 2are the radii of the donor and acceptor, r 12is the donor–acceptor distance, ε is the dielectric constant, and n is the refractive index [6,40].

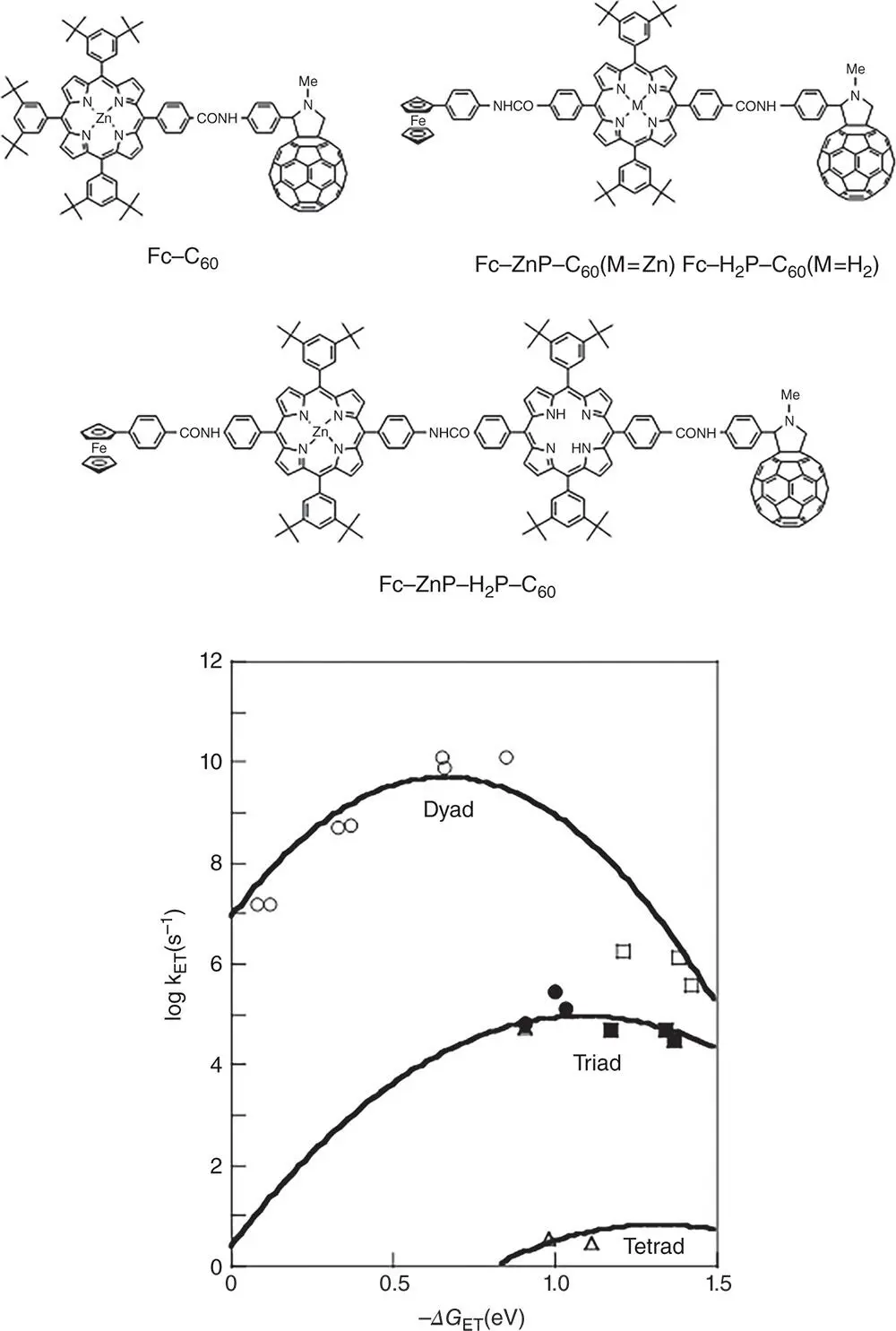
Figure 3.1Driving force (−Δ G ET) dependence of intramolecular electron‐transfer rate constants ( k ET) in ZnP–C 60(CS [○]; CR [□]), Fc–ZnP–C 60(•), Fc–H 2P–C 60(▴), ZnP–H 2P–C 60(▪), and Fc–ZnP–H 2P–C 60(△).

Source: Imahori et al. 2001 [39]. Reproduced with permission of American Chemical Society.

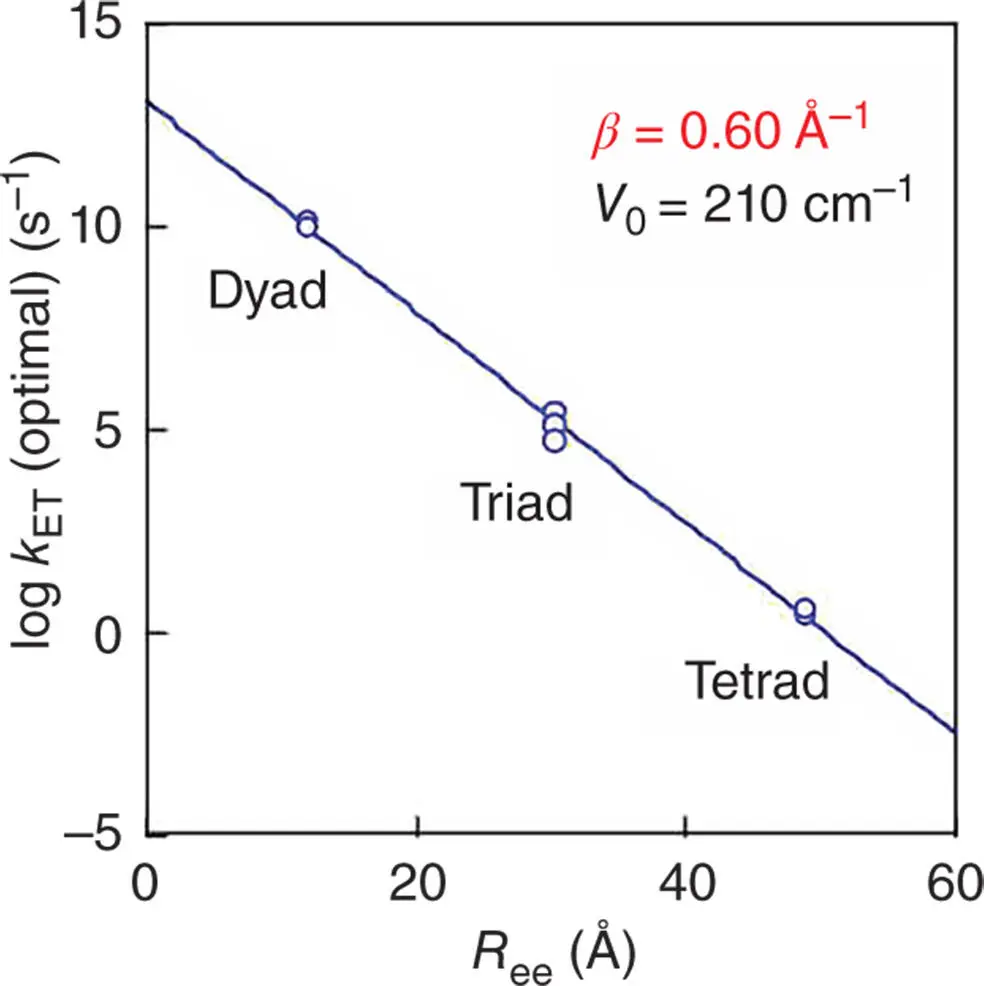
Figure 3.2Edge‐to‐edge distance ( R ee) dependence of optimal electron‐transfer rate constants (log[ k ET(optimal)/s −1]) in ZnP–C 60dyad, Fc–ZnP–C 60triad, Fc–H 2P–C 60triad, ZnP–H 2P–C 60triad, and Fc–ZnP–H 2P–C 60tetrad. The line represents the best fit to Eq. (2.1) ( β = 0.60 Å −1, V 0= 210 cm −1).

In the case of the dyad, the CR rate in ZnP ·+–C 60 ·−in the Marcus inverted region is much slower than the CS rate constants from both the singlet and triplet excited states in the Marcus normal region (Figure 3.1). This enables subsequent electron transfer from Fc to ZnP ·+in the triad (Fc–ZnP ·+–C 60 ·−) and from ZnP to H 2P ·+in ZnP–H 2P ·+–C 60 ·−to produce the final CS state, Fc +–ZnP–C 60 ·−and ZnP ·+–H 2P–C 60 ·−, in competition with the back electron transfer in the initial CS states. In the case of Fc +–ZnP–H 2P–C 60 ·−, the charges are separated at a long distance ( R ee= 48.9 Å) [39]. The lifetime of the resulting CS state at such a long distance in a frozen benzonitrile (PhCN) has been determined as 0.38 seconds [39]. Similar tetrad and pentad compounds were reported to attain long‐lived CS states up to 1.7 seconds [40–42]. It should be noted that the CS lifetime is temperature independent, since the CR process is at the Marcus top region (Figure 3.1) [39]. This is the first example to achieve a CS lifetime that is comparable to that observed for the bacterial photosynthetic reaction center. However, such an extremely long CS lifetime could only be determined in frozen media, since in condensed media bimolecular back electron transfer between two Fc +–ZnP–H 2P–C 60 ·−is much faster than the unimolecular CR process [39]. The maximum k ETvalues ( k ETmax) of dyads, triads, and tetrads in the Marcus plot (Figure 3.2) are correlated with the edge‐to‐edge distance ( R ee), separating the radical ions, according to Eq. (3.2)[39]: