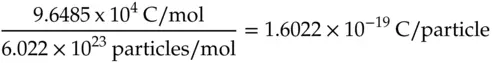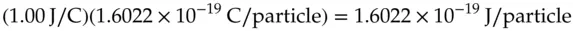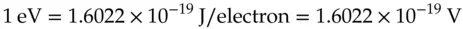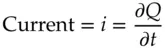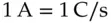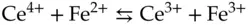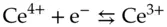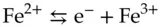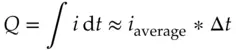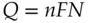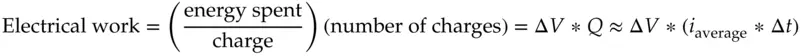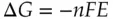Gary A. Mabbott - Electroanalytical Chemistry

(1.2)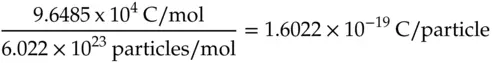

This value is the charge on an electron and is known as the elementary charge. One can calculate the energy that would be required to move a single electron through a voltage difference of 1 V by multiplying the elementary charge by 1 V in the units of 1 J/C:

(1.3)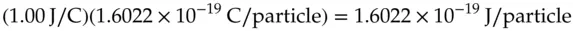

The result of this calculation is frequently useful and provides the definition for a separate unit of electric potential energy per elementary charge, namely, the electron‐volt, eV.

(1.4)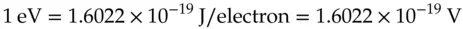

Current describes the movement of charge. It is the measure of the rate of change in charge moving past a specific observation point.

(1.5)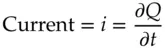

where Q is the charge in coulombs and time, t , is in seconds. Current has the units of coulombs per second or amperes.

(1.6)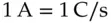

If one were to make the analogy of an electrical circuit with a river, then the current in amperes or coulombs per second parallels the volume flow rate of the river in gallons per second. The potential energy difference or voltage that is associated with any given component (such as an electrode in an electrochemical experiment) in the electrical circuit, is analogous to the energy available to do work per gallon of water as it drops over a waterfall. Current describes the rate of charge moving (amount per unit of time) and potential is a measure of the energy per unit charge in moving between two points.

The exchange of electrons between two chemical species is generally known as an oxidation/reduction process or redox reaction. In a redox reaction occurring in a homogeneous solution, one reactant gains electrons while the other reactant loses. It is often useful to consider a redox reaction from the perspective of one of the reactants. Consider a redox reaction between cerium and iron ions in aqueous solution:

(1.7)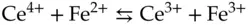

The net reaction equation does not show any electrons as either reactants or products. However, it is useful to separate the two reactants into “half reactions” where electrons do appear.

(1.8)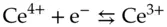

(1.9)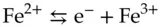

A process in which a chemical species accepts one or more electrons is known as a reduction reaction; a process in which a species loses electrons is an oxidation reaction. Writing the half reactions indicates that the Fe 2+ion is being oxidized and the Ce 4+ion is being reduced. It also clearly states how many electrons are being transferred per mole of a given reactant.

In many instrumental electrochemical methods, an electrode surface – usually a metal or carbon conductor – exchanges electrons with the analyte. In those cases, the electrode is treated as an inert source or sink for the electron exchange. The electrode does not appear in the reaction equation. Instead, the electrode reaction appears to be the same as the half reaction for the species being converted. A major benefit of using electrodes in place of a reagent in solution is the fact that the current passing through the electrode can be measured unlike the situation when two chemical species in solution exchange electrons directly. Furthermore, the current is a measure of the amount of analyte reacting. Whenever electrons are transferred between the analyte and an electrode, the current can be integrated with respect to time in order to obtain the charge, Q , transferred.

(1.10)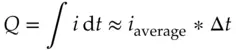

This charge is related to the moles of oxidized or reduced species by Faraday's law:

(1.11)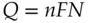

where n = number of moles of electrons transferred per mole of reactant, N is the number of moles of the same reactant that undergo conversion, and F is Faraday's constant, 9.6485 x 10 4C/mol of electrons.

If charge is moved, the amount of work done is proportional to the difference in voltage. Because the voltage difference, Δ V , is the energy spent per unit charge, the total work done in moving the charge, Q , is

(1.12)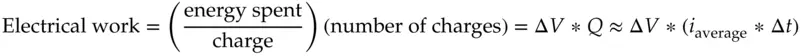

This is analogous to carrying a piano up a flight of stairs. The potential energy difference is fixed by the height of the stairs. To move two pianos requires twice the amount of work.

There are a couple of other conventions worth mentioning here. In electrochemical contexts, E is used instead of Δ V to represent the electrochemical potential energy difference. It is also common to equate electrical work and the Gibb's free energy change, Δ G . The relationship between potential and Δ G is usually expressed in terms of the energy per mole of reactant:

( 1.13)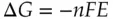

where n is the number of moles of electrons/mol of reactant, F is Faraday's constant in coulombs/mol of electrons, and E is the potential difference in volts or joules/coulomb. A dimension analysis indicates that Δ G in Eq. (1.13)has the units of joules per mole of reactant. To find the total energy spent/released, or the total work done, one needs to multiply Eq. (1.13)by N , the number of moles of reactant being converted. Also, note that it is a matter of convention that favorable electrochemical processes are assigned positive potentials. Thus, the sign in Eq. (1.13)yields a negative Δ G for a positive value of E for a favorable process.

Another convention is to define the direction of a current as the direction that the positive charges move. This is the case, despite the fact that electrons are usually the major charge carriers and are moving in the opposite direction. That means that a current flows from a point of a higher potential to a point of lower potential; the electrons move in the opposite direction.